题目内容
已知命题：若数列{an}为等差数列，且am=a，an=b（m≠n，m、n∈N*），则am+n=
；现已知等比数列{bn}（bn＞0，n∈N*），bm=a，bn=b（m≠n，m、n∈N*），若类比上述结论，则可得到bm+n=______．
| bn-am |
| n-m |
等差数列中的bn和am可以类比等比数列中的bn和am，
等差数列中的bn-am可以类比等比数列中的
，
等差数列中的
可以类比等比数列中的
．
故bm+n=
，
故答案为
．
等差数列中的bn-am可以类比等比数列中的
| bn |
| am |
等差数列中的
| bn-am |
| n-m |
| n-m |
| ||
故bm+n=
| n-m |
| ||
故答案为
| n-m |
| ||
练习册系列答案
相关题目
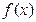定义域中任意的
(
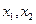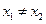)，有如下结论：
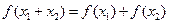；（2）
；
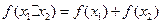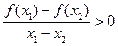；（4）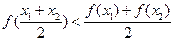
；试分别写出对应上述一个结论成立的四个函数：
，
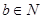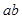能被5整除，则a，b中至少有一个能被5整除”，那么假设的内容是( )