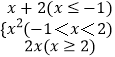题目内容
【题目】函数f(x)是定义在R上的减函数,且f(x)>0恒成立,若对任意的x,y∈R,都有f(x﹣y)= ![]() ,
,
(1)求f(0)的值,并证明对任意的x,y∈R,f(x+y)=f(x)f(y);
(2)若f(﹣1)=3,解不等式 ![]() ≤9.
≤9.
【答案】
(1)解:令x=0,y=0得f(0)= ![]() =1,
=1,
∴f(0)=1
令x=a+b,y=b,则x﹣y=a,
又∵f(x﹣y)= ![]() ,
,
∴f(a+b)=f(a)f(b)
∴f(x+y)=f(x)f(y)
(2)解:由(1)知f(x2)f(10)=f(x2+10),
∴ ![]() =
= ![]() =f(x2﹣7x+10),
=f(x2﹣7x+10),
又∵f(﹣1)=3,∴9=3×3=f(﹣1)×f(﹣1)=f(﹣2)
又∵ ![]() ≤9.
≤9.
∴f(x2﹣7x+10)≤f(﹣2)
又∵f(x)在R上单调递减,
∴x2﹣7x+10≥﹣2
解得:x≤3或x≥4,即原不等式的解集为(﹣∞,3)∪(4,+∞)
【解析】(1)利用赋值法结合条件进行转化求解证明即可.(2)根据抽象函数的关系进行转化,结合函数单调性进行求解即可.

练习册系列答案
相关题目