题目内容
【题目】如图,已知圆锥![]() 和圆柱
和圆柱![]() 的组合体(它们的底面重合),圆锥的底面圆
的组合体(它们的底面重合),圆锥的底面圆![]() 半径为
半径为![]() ,
, ![]() 为圆锥的母线,
为圆锥的母线, ![]() 为圆柱
为圆柱![]() 的母线,
的母线, ![]() 为下底面圆
为下底面圆![]() 上的两点,且
上的两点,且![]() ,
, ![]() ,
, ![]() .
.

(1)求证:平面![]() 平面
平面![]() ;
;
(2)求二面角![]() 的正弦值.
的正弦值.
【答案】(1)见解析(2)![]()
【解析】试题分析:(1)先根据平几知识计算得![]() ,再根据圆柱性质得
,再根据圆柱性质得![]() 平面
平面![]() ,即有
,即有![]() ,最后根据线面垂直判定定理得
,最后根据线面垂直判定定理得![]() 平面
平面![]() ,即得平面
,即得平面![]() 平面
平面![]() ;(2)求二面角,一般利用空间向量进行求解,先根据条件建立空间直角坐标系,设立各点坐标,利用方程组解出各面法向量,利用向量数量积求法向量夹角,最后根据二面角与向量夹角之间关系求解
;(2)求二面角,一般利用空间向量进行求解,先根据条件建立空间直角坐标系,设立各点坐标,利用方程组解出各面法向量,利用向量数量积求法向量夹角,最后根据二面角与向量夹角之间关系求解
试题解析:解:(1)依题易知,圆锥的高为![]() ,又圆柱的高为
,又圆柱的高为![]() ,
,
所以![]() ,
,
因为![]() ,所以
,所以![]() ,
,
连接![]() ,易知
,易知![]() 三点共线,
三点共线, ![]() ,
,
所以![]() ,
,
所以![]() ,
,
解得![]() ,又因为
,又因为![]() ,圆
,圆![]() 的直径为10,圆心
的直径为10,圆心![]() 在
在![]() 内,
内,
所以易知![]() ,所以
,所以![]() .
.
因为![]() 平面
平面![]() ,所以
,所以![]() ,因为
,因为![]() ,所以
,所以![]() 平面
平面![]() .
.
又因为![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() .
.
(2)如图,以![]() 为原点,
为原点, ![]() 、
、![]() 所在的直线为
所在的直线为![]() 轴,建立空间直角坐标系.
轴,建立空间直角坐标系.
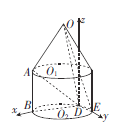
则![]() .
.
所以![]() ,
,
设平面![]() 的法向理为
的法向理为![]() ,
,
所以![]() ,令
,令![]() ,则
,则![]() .
.
可取平面![]() 的一个法向量为
的一个法向量为![]() ,
,
所以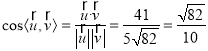 ,
,
所以二面角![]() 的正弦值为
的正弦值为![]() .
.

【题目】某花店每天以每枝5元的价格从花市购进若干枝玫瑰花,然后以每枝10元的价格出售.如果当天卖不完,剩下的玫瑰花作垃圾处理.
(1)若花店一天购进17支玫瑰花,求当天的利润![]() (单位:元),关于当天需求量
(单位:元),关于当天需求量![]() (单位:枝,
(单位:枝, ![]() 的解析式;
的解析式;
(2)花店记录了100天玫瑰花的日需求量(单位:枝),整理得如表:
日需求量 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
频数 | 10 | 20 | 16 | 16 | 15 | 13 | 10 |
①假设花店在这100天内每天购进16枝玫瑰花或每天购进17枝玫瑰花,分别计算这100天花店的日利润(单位:元)的平均数,并以此作为决策依据,花店在这100天内每天购进16枝还是17枝玫瑰花?
②若花店一天购进17枝玫瑰花,以100天记录的各需求量的频率作为概率,求当天的利润不少于75元的概率.
【题目】为提高市场销售业绩,某公司设计两套产品促销方案(方案1运作费用为![]() 元/件;方案2的的运作费用为
元/件;方案2的的运作费用为![]() 元/件),并在某地区部分营销网点进行试点(每个试点网点只采用一种促销方案),运作一年后,对比该地区上一年度的销售情况,分别统计相应营销网点个数,制作相应的列联表如下表所示.
元/件),并在某地区部分营销网点进行试点(每个试点网点只采用一种促销方案),运作一年后,对比该地区上一年度的销售情况,分别统计相应营销网点个数,制作相应的列联表如下表所示.
无促销活动 | 采用促销方案1 | 采用促销方案2 | ||
本年度平均销售额不高于上一年度平均销售额 | 48 | 11 | 31 | 90 |
本年度平均销售额高于上一年度平均销售额 | 52 | 69 | 29 | 150 |
100 | 80 | 60 |
(Ⅰ)请根据列联表提供的信息,为该公司今年选择一套较为有利的促销方案(不必说明理由);
(Ⅱ)已知该公司产品的成本为10元/件(未包括促销活动运作费用),为制定本年度该地区的产品销售价格,统计上一年度的![]() 组售价
组售价![]() (单位:元/件,整数)和销量
(单位:元/件,整数)和销量![]() (单位:件)(
(单位:件)(![]() )如下表所示:
)如下表所示:
售价 |
|
|
|
|
|
|
|
|
销量 |
|
|
|
|
|
|
|
|
(ⅰ)请根据下列数据计算相应的相关指数![]() ,并根据计算结果,选择合适的回归模型进行拟合;
,并根据计算结果,选择合适的回归模型进行拟合;
(ⅱ)根据所选回归模型,分析售价![]() 定为多少时?利润
定为多少时?利润![]() 可以达到最大.
可以达到最大.
|
|
| |
|
|
|
|
|
| ||
参考公式:相关指数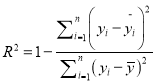 .
.