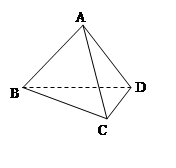
题目内容
（12分）已知三棱锥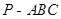
各侧棱长均为
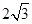，三个顶角均为
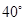，M,N分别为PA,PC上的点，求
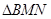周长的最小值.
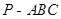各侧棱长均为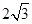，三个顶角均为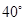，M,N分别为PA,PC上的点，求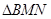周长的最小值.6
本小题属于侧面展开的问题.平面中，两点间的线段距离最短.将棱锥侧面沿PB剪开，展开成平面图形，设边界为PB ,PB'
则∠BPB'=120°,连接BB',则与PA ,PC 的交点即为MN，最小值为BB'
利用余弦定理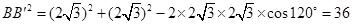
,
所以BB'=6,即三角形BMN周长最小值是6.
则∠BPB'=120°,连接BB',则与PA ,PC 的交点即为MN，最小值为BB'
利用余弦定理
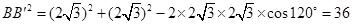,所以BB'=6,即三角形BMN周长最小值是6.
练习册系列答案
相关题目
a(0<
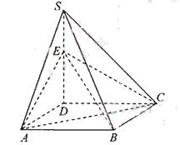
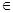（0、1），都有AC⊥BE:
中，点
在线段
上移动，则异面直线
与
所成的角
的取值范围( )
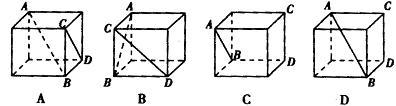
的面积为8,当矩形周长取最小值时,沿对角线
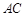把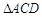
折起,则三棱锥
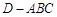的外接球的表面积为________
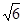，则球的体积是_________.
，
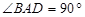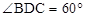，BC⊥CD .