题目内容
若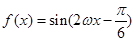 的图象关于直线
的图象关于直线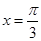 对称,其中
对称,其中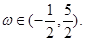
(1)求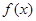 的解析式;
的解析式;
(2)将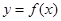 的图象向左平移
的图象向左平移 个单位,再将得到的图象的横坐标变为原来的2倍(纵坐标不变)后得到
个单位,再将得到的图象的横坐标变为原来的2倍(纵坐标不变)后得到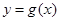 的图象;若函数
的图象;若函数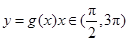 的图象与
的图象与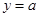 的图象有三个交点且交点的横坐标成等比数列,求
的图象有三个交点且交点的横坐标成等比数列,求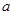 的值.
的值.
(1)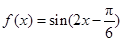 ;(2)
;(2)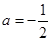 .
.
解析试题分析:(1)本题考查了三角函数的对称性,利用通解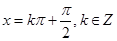 来求解;(2)由图象变换求得
来求解;(2)由图象变换求得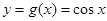 ,再利用三交点的横坐标成等比数列求得
,再利用三交点的横坐标成等比数列求得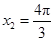 ,因此
,因此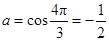 .此题将数列与三角函数知识联系在一起,在知识的交汇处命题.
.此题将数列与三角函数知识联系在一起,在知识的交汇处命题.
试题解析:(1)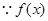 的图象关于直线
的图象关于直线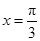 对称,
对称,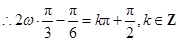 ,解得
,解得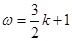 , 2分
, 2分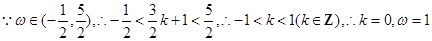
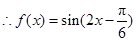 5分
5分
(2)将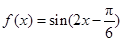 的图象向左平移
的图象向左平移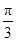 个单位后,提到
个单位后,提到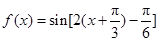
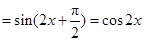 ,再将得到的图象的横坐标变为原来的2倍(纵坐标不变)后,得到
,再将得到的图象的横坐标变为原来的2倍(纵坐标不变)后,得到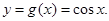 9分
9分
函数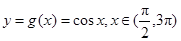 的图象与
的图象与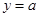 的图象有三个交点坐标分别为
的图象有三个交点坐标分别为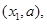
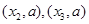 且
且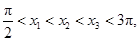
则由已知结合图象的对称性,有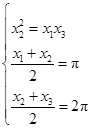 ,解得
,解得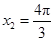 11分
11分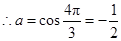 . 12分
. 12分
考点:1.三角函数解析式的求解;2.函数的对称性;3.三角函数图象的变换;4.等比中项.

练习册系列答案
相关题目
 cosx,cosx),设函数f(x)=a•b-
cosx,cosx),设函数f(x)=a•b- , 且α∈(
, 且α∈( ,π). 求α.
,π). 求α.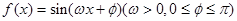 为偶函数,周期为2
为偶函数,周期为2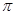 .
.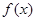 的解析式;
的解析式;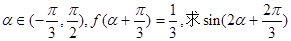 的值.
的值.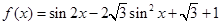 .
. 的最小正周期;
的最小正周期;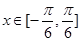 时,求
时,求 ,
, ,且
,且 ,其中A、B、C是
,其中A、B、C是 ABC的内角,
ABC的内角, 分别是角A,B,C的对边。
分别是角A,B,C的对边。 的取值范围;
的取值范围;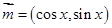 和
和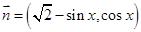 ,
,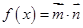 ,写出函数
,写出函数 的最小正周期;并求函数
的最小正周期;并求函数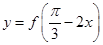 的单调区间;
的单调区间;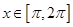 ,求
,求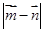 的最大值.
的最大值. 的图象过点(0,
的图象过点(0,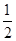 ),最小正周期为
),最小正周期为 ,且最小值为-1.
,且最小值为-1. 的解析式.
的解析式. ,
, ,求m的取值范围.
,求m的取值范围. ,中心角
,中心角 .求证:当
.求证:当 时该扇形面积最大;
时该扇形面积最大;
 .求证:
.求证: .
.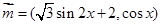 ,
,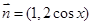 设函数
设函数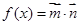 .
. 求
求 的最小正周期与单调递增区间;
的最小正周期与单调递增区间; 在
在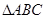 中,
中,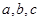 分别是角
分别是角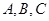 的对边,若
的对边,若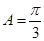 ,
,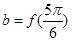 ,
,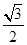 ,求
,求 的值.
的值.