题目内容
已知向量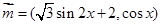 ,
,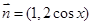 设函数
设函数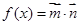 .
. 求
求 的最小正周期与单调递增区间;
的最小正周期与单调递增区间; 在
在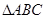 中,
中,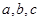 分别是角
分别是角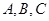 的对边,若
的对边,若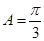 ,
,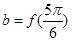 ,
,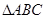 的面积为
的面积为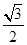 ,求
,求 的值.
的值.

 的最小正周期
的最小正周期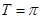 ,单调递增区间为
,单调递增区间为 ;
;
 .
.
解析试题分析: 利用向量数量积的坐标运算及三角恒等变换得到
利用向量数量积的坐标运算及三角恒等变换得到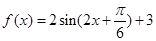 ,可得最小正周期为
,可得最小正周期为 .利用复合函数的单调性得单调递增区间
.利用复合函数的单调性得单调递增区间
 先由
先由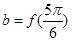 计算出b=2,结合
计算出b=2,结合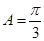 由面积公式
由面积公式 ,最后由余弦定理得
,最后由余弦定理得 .
.
试题解析:(Ⅰ)
 3分
3分
∴ 的最小正周期
的最小正周期 4分
4分
由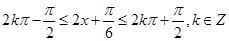 得
得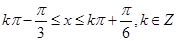
∴ 的单调递增区间为
的单调递增区间为 6分
6分
(Ⅱ)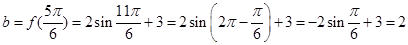 8分
8分 10分
10分
在 中,由余弦定理得
中,由余弦定理得
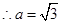 12分
12分
考点:1.平面向量的坐标运算;2.三角恒等变换;3.三角形面积公式;4.余弦定理.

练习册系列答案
相关题目
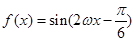 的图象关于直线
的图象关于直线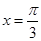 对称,其中
对称,其中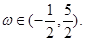
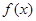 的解析式;
的解析式;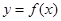 的图象向左平移
的图象向左平移 个单位,再将得到的图象的横坐标变为原来的2倍(纵坐标不变)后得到
个单位,再将得到的图象的横坐标变为原来的2倍(纵坐标不变)后得到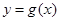 的图象;若函数
的图象;若函数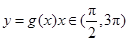 的图象与
的图象与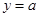 的图象有三个交点且交点的横坐标成等比数列,求
的图象有三个交点且交点的横坐标成等比数列,求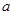 的值.
的值. ,若
,若 的最大值为1.
的最大值为1.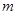 的值,并求
的值,并求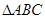 中,角
中,角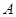 、
、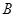 、
、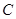 的对边
的对边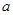 、
、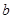 、
、 ,若
,若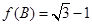 ,且
,且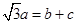 ,试判断三角形的形状.
,试判断三角形的形状.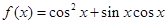 .
. 的最小正周期和最小值;
的最小正周期和最小值; 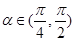 且
且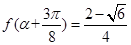 ,求
,求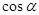 的值.
的值.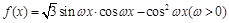 的最小正周期为
的最小正周期为 .
. 的解析式;
的解析式;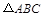 的三边
的三边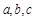 满足
满足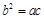 ,且边
,且边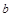 所对的角为
所对的角为 ,求此时函数
,求此时函数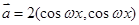 ,
,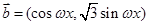 (其中
(其中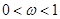 ),函数
),函数 ,若直线
,若直线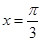 是函数
是函数 图象的一条对称轴.
图象的一条对称轴.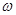 的值;
的值;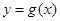 的图象是由
的图象是由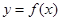 的图象的各点的横坐标伸长到原来的2倍,然后再向左平移
的图象的各点的横坐标伸长到原来的2倍,然后再向左平移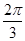 个单位长度得到,求
个单位长度得到,求 ,
,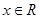 .
. 的最小值和最小正周期;
的最小值和最小正周期;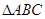 的内角
的内角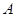 、
、 、
、 的对边分别为
的对边分别为 、
、 、
、 ,满足
,满足 ,
,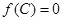 且
且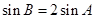 ,求
,求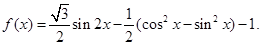
 的最小值和最小正周期;
的最小值和最小正周期;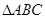 的内角
的内角 、
、 、
、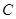 的对边分别为
的对边分别为 、
、 、
、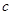 且
且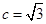 ,
,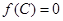 ,若向量
,若向量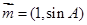 与向量
与向量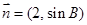 共线,求
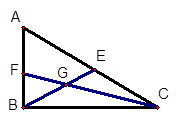
共线,求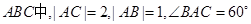 ,G是三角形
,G是三角形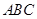 的重心,求
的重心,求 .
.
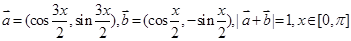 ,求x。
,求x。