题目内容
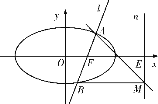
【题目】如图,椭圆C:![]() 的右焦点为F,过点F的直线l与椭圆交于A、B两点,直线n:x=4与x轴相交于点E,点M在直线n上,且满足BM∥x轴.
的右焦点为F,过点F的直线l与椭圆交于A、B两点,直线n:x=4与x轴相交于点E,点M在直线n上,且满足BM∥x轴.
(1)当直线l与x轴垂直时,求直线AM的方程;
(2)证明:直线AM经过线段EF的中点.
【答案】(1) 直线AM的方程为y=-x+![]() 或y=x-
或y=x-![]() ;(2)见证明
;(2)见证明
【解析】
(1)直线l与x轴垂直,可得直线l的方程,从而求解出点![]() 的坐标,由BM∥x轴可得
的坐标,由BM∥x轴可得![]() 点坐标,从而得出直线AM的方程;
点坐标,从而得出直线AM的方程;
(2)要证直线AM经过线段EF的中点![]() ,即证A,N,M三点共线,即证
,即证A,N,M三点共线,即证![]() ,设出
,设出![]() 两点,联立直线与椭圆的方程,借助韦达定理从而得证.
两点,联立直线与椭圆的方程,借助韦达定理从而得证.
解:(1)由c=![]() =1,
=1,
∴F(1,0),
∵直线l与x轴垂直,
∴x=1,
由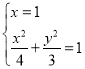 ,
,
解得: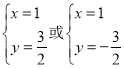
故当点![]() 坐标为
坐标为![]() ,
,
则点![]() 坐标为
坐标为![]() ,
,
此时直线AM的斜率为 ,
,
直线AM的方程为![]() ,
,
∴直线AM的方程为y=-x+![]() ;
;
当点![]() 坐标为
坐标为![]() ,
,
则点![]() 坐标为
坐标为![]() ,
,
此时直线AM的斜率为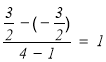 ,
,
直线AM的方程为![]() ,
,
∴直线AM的方程为y=x-![]() ;
;
故直线AM的方程为y=-x+![]() 或y=x-
或y=x-![]() ;
;
(2)当![]() 直线方程为
直线方程为![]() 时,
时,
直线BM与x轴重合,不满足题意;
故可设直线l的方程为x=my+1,
由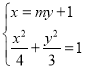 ,
,
得3(my+1)2+4y2=12,
(3m2+4)y2+6my-9=0,
设A(x1,y1),B(x2,y2),
由韦达定理可得,
y1+y2=![]() ,y1y2=
,y1y2=![]()
∵EF的中点N![]() ,点M(4,y2),
,点M(4,y2),
∴![]() =
=![]()
![]() ×y2-
×y2-![]() y1=my1y2-
y1=my1y2-![]() (y1+y2)=
(y1+y2)=![]() -
-![]() ×
×![]() =0.
=0.
所以![]() ,
,
故A,N,M三点共线,
所以直线AM经过线段EF的中点.

练习册系列答案
相关题目