Question

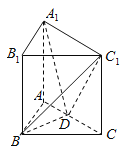
【题目】如图，在直三棱柱中，平面侧面，且，

（Ⅰ）求证：；

（Ⅱ）若直线与平面所成角的大小为，求锐二面角的大小．

Answer 1

【答案】（Ⅰ）详见解析；（Ⅱ）.

【解析】

（Ⅰ）先取的中点，连接，根据线面垂直的判定定理，证明侧面，进而可得出；

(Ⅱ)根据（Ⅰ）的结果，得到且底面，以点为原点，以所在直线分别为， ，轴建立空间直角坐标系，设，表示出，再求出平面的一个法向量，根据直线与平面所成角的大小为，求出，再求出平面的一个法向量，由向量夹角公式，即可求出结果.

（Ⅰ）如图，取的中点，连接.

因为，所以.

由平面侧面，且平面侧面，

得平面.

又平面，所以，

因为三棱柱是直三棱柱，则底面，所以

又，从而侧面，

又侧面，故．

(Ⅱ)由（1）知且底面，所以以点为原点，以所在直线分别为， ，轴建立空间直角坐标系.

设，则，，，，，，，.

设平面的一个法向量，由，，得.

令，得，则.

设直线与平面所成的角为，则，

所以，

解得， 即.

又设平面的一个法向量为，同理可得.

设锐二面角的大小为，则，

由，得.

∴锐二面角的大小为.