题目内容
如图,在长方体ABCD-A1B1C1D1中,底面ABCD是边长为![]() 的正方形,AA1=
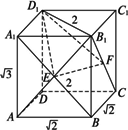
的正方形,AA1=![]() ,E、F分别是AB1、CB1的中点,求证:平面D1EF⊥平面AB1C
,E、F分别是AB1、CB1的中点,求证:平面D1EF⊥平面AB1C
答案:
解析:
提示:
解析:
|
证明:如图,设AC∩BD=O,连结B1O,交EF于点M.
∵AE=EB1,CF=FB1, ∴EF 又∵AB1=CB1,O是AC的中点, ∴B1O⊥AC. ∵EF∥AC,∴B1O⊥EF. 在Rt△B1OB中, B1O= ∴B1M= ∵四边形D1DBB1为平行四边形,D1B1∥DB, ∴∠D1B1O=∠BOB1. ∵B1D1=2=B1O,B1M=OB=1,且∠D1B1M=∠BOB1,∴△D1B1M≌△B1OB ∴∠D1MB1=∠B1BO. ∵∠B1BO=90°, ∴∠D1MB1=90°. ∴B1M⊥D1M,即B1O⊥D1M. ∵B1O⊥EF,D1M∩EF=M, ∴B1O⊥平面D1EF. ∵B1O ∴平面D1EF⊥平面AB1C 思路分析:此题中B1O⊥EF较易得到,而证B1O⊥D1M则通过了较复杂数据的关系及三角形知识才能完成.平时做题经常会遇到此类情况 |
提示:
|
要证两平面垂直,最常用的办法是证一个平面内的一条直线垂直于另一平面,而线垂直面的证明关键在于找到面内有两条相交直线垂直已知直线.要善于运用题目给出的信息,通过计算挖掘题目的垂直与平行关系,这是一种非常重要的思想方法,它可以使复杂问题简单化. |

练习册系列答案
相关题目

 如图在长方体ABCD-A1B1C1D1中,三棱锥A1-ABC的面是直角三角形的个数为:
如图在长方体ABCD-A1B1C1D1中,三棱锥A1-ABC的面是直角三角形的个数为: 如图,定义八个顶点都在某圆柱的底面圆周上的长方体叫做圆柱的内接长方体,圆柱也叫长方体的外接圆柱.设长方体ABCD-A1B1C1D1的长、宽、高分别为a,b,c(其中a>b>c),那么该长方体的外接圆柱侧面积的最大值等于( )
如图,定义八个顶点都在某圆柱的底面圆周上的长方体叫做圆柱的内接长方体,圆柱也叫长方体的外接圆柱.设长方体ABCD-A1B1C1D1的长、宽、高分别为a,b,c(其中a>b>c),那么该长方体的外接圆柱侧面积的最大值等于( )

 .
. 
 ,AA1 =
,AA1 = ,M为侧棱CC1上一点,AM⊥BA1.
,M为侧棱CC1上一点,AM⊥BA1.