Question

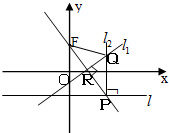
如图，在平面直角坐标系xoy中，设点F（0，p）（p＞0），直线l：y=-p，点p在直线l上移动，R是线段PF与x轴的交点，过R、P分别作直线l₁、l₂，使l₁⊥PF，l₂⊥ll₁∩l₂=Q．
（Ⅰ）求动点Q的轨迹C的方程；
（Ⅱ）在直线l上任取一点M做曲线C的两条切线，设切点为A、B，求证：直线AB恒过一定点；
（Ⅲ）对（Ⅱ）求证：当直线MA，MF，MB的斜率存在时，直线MA，MF，MB的斜率的倒数成等差数列．

Answer 1

（Ⅰ）依题意知，点R是线段FP的中点，且RQ⊥FP，
∴RQ是线段FP的垂直平分线．---------------------------------------（2分）
∴|PQ|=|QF|．
∴动点Q的轨迹C是以F为焦点，l为准线的抛物线，其方程为：x²=4py（p＞0）．--------------------（4分）
（Ⅱ）证明：设M（m，-p），两切点为A（x₁，y₁），B（x₂，y₂）
由x²=4py得y=

1

4p

x2，求导得y′=

1

2p

x．
∴两条切线方程为y-y1=

1

2p

x1(x-x1)①
y-y2=

1

2p

x2(x-x2)②-------------------（6分）
对于方程①，代入点M（m，-p）得，-p-y1=

1

2p

x1(m-x1)，
又y1=

1

4p

x12
∴-p-

1

4p

x12=

1

2p

x1(m-x1)
整理得：x12-2mx1-4p2=0
同理对方程②有x22-2mx2-4p2=0
即x₁，x₂为方程x²-2mx-4p²=0的两根．
∴x₁+x₂=2m，x₁x₂=-4p²③-----------------------（8分）
设直线AB的斜率为k，k=

y2-y1

x2-x1

=

1

4p

(x1+x2)
所以直线AB的方程为y-

1

4p

x12=

1

4p

(x1+x2)(x-x1)，展开得：y=

1

4p

(x1+x2)x-

x1x2

4p

，
代入③得：y=

m

2p

x+p
∴直线恒过定点（0，p）．-------------------------------------（10分）
（Ⅲ）证明：由（Ⅱ）的结论，设M（m，-p），A（x₁，y₁），B（x₂，y₂）
且有x₁+x₂=2m，x₁x₂=-4p²，
∴k_MA=

y1+p

x1-m

，k_MB=

y2+p

x2-m

----------------------------（11分）
∴

1

kMA

+

1

kMB

=

1

y1+p x1-m

+

1

y2+p x2-m

=

4pm

x1x2

=

4pm

-4p2

=-

m

p

------（13分）
又∵

1

kMF

=

m

-p-p

=-

m

2p

，
∴

1

kMA

+

1

kMB

=

2

kMF

即直线MA，MF，MB的斜率的倒数成等差数列．----------------------------（14分）