题目内容
5.已知tanθ=2,则sin2θ-sinθcosθ+cos2θ=$\frac{3}{5}$.分析 由条件利用同角三角函数的基本关系求得所给式子的值.
解答 解:∵tanθ=2,则sin2θ-sinθcosθ+cos2θ=$\frac{{sin}^{2}θ-sinθcosθ{+cos}^{2}θ}{{sin}^{2}θ{+cos}^{2}θ}$
=$\frac{{tan}^{2}θ-tanθ+1}{{tan}^{2}θ+1}$=$\frac{4-2+1}{4+1}$=$\frac{3}{5}$,
故答案为:$\frac{3}{5}$.
点评 本题主要考查同角三角函数的基本关系的应用,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.已知一几何体的三视图如图所示,则该几何体的体积是( )
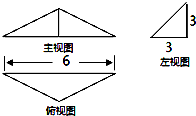

| A. | 6 | B. | 9 | C. | 12 | D. | 18 |
20.某学习兴趣小组开展“学生语文成绩与英语成绩的关系”的课题研究,对该校高二年级800名学生上学期期末语文和英语成绩进行统计,按优秀和不优秀进行分类.记集合A={语文成绩优秀的学生},B={英语成绩优秀的学生}.如果用card(M)表示有限集合M中元素的个数.已知card(A∩B)=60,card(A∩CUB)=140,card(CUA∩B)=100,其中U表示800名学生组成的全集.
(Ⅰ)是否有99.9%的把握认为“该校学生的语文成绩与英语成绩优秀与否有关系”;
(Ⅱ)将上述调查所得的频率视为概率,从该校高二年级的学生成绩中,有放回地随机抽取3次,记所抽取的成绩中,语文英语两科成绩中至少有一科优秀的人数为x,求x的分布列和数学期望.
附:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$
参考数据:
(Ⅰ)是否有99.9%的把握认为“该校学生的语文成绩与英语成绩优秀与否有关系”;
(Ⅱ)将上述调查所得的频率视为概率,从该校高二年级的学生成绩中,有放回地随机抽取3次,记所抽取的成绩中,语文英语两科成绩中至少有一科优秀的人数为x,求x的分布列和数学期望.
附:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$
参考数据:
| P(K2≥k0) | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 5.024 | 6.635 | 7.879 | 10.828 |
10.若复数z=2-i ( i为虚数单位),则$\frac{10}{z}$=( )
| A. | 4+2i | B. | 20+10i | C. | 4-2i | D. | $\frac{20}{3}+\frac{10}{3}i$ |
17.复数z=$\frac{m+i}{1+i}$(m∈R,i为虚数单位)在复平面上对应的点不可能位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
14.双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的离心率为2,焦点到渐近线的距离为$\sqrt{3}$,则C的焦距等于( )
| A. | 2 | B. | 2$\sqrt{2}$ | C. | 2$\sqrt{3}$ | D. | 4 |