题目内容
17．复数z=$\frac{m+i}{1+i}$（m∈R，i为虚数单位）在复平面上对应的点不可能位于（ ）| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |
分析 通过化简复数z，比较即可．
解答 解：z=$\frac{m+i}{1+i}$=$\frac{（m+i）（1-i）}{（1+i）（1-i）}$=$\frac{m+（1-m）i-{i}^{2}}{1-{i}^{2}}$=$\frac{1+m}{2}$+$\frac{1-m}{2}$i，
当1+m＞0且1-m＞0时，有解：-1＜m＜1；
当1+m＞0且1-m＜0时，有解：m＞1；
当1+m＜0且1-m＞0时，有解：m＜-1；
当1+m＜0且1-m＜0时，无解；
故选：C．
点评 本题考查复数的几何意义，注意解题方法的积累，属于中档题．
练习册系列答案
提分百分百检测卷系列答案
相关题目
8．定义在R上的偶函数f（x）满足f（x+2）-f（x）=0，且在[-1，0]上单调递增，设a=f（log32），b=f（-$\frac{1}{3}$log32），c=f（$\frac{19}{12}$），则a，b，c的大小关系是（ ）
| A． | a＞b＞c | B． | a＞c＞b | C． | b＞c＞a | D． | c＞b＞a |
12．已知函数f（x）=2ax3-3x2+1，若 f（x）存在唯一的零点x0，且x0＞0，则a的取值范围是（ ）
| A． | （1，+∞） | B． | （0，1） | C． | （-1，0） | D． | （-∞，-1） |
9．直线2x-5y+20=0与坐标轴交于两点，以坐标轴为对称轴，以其中一个点为焦点且另一个点为虚轴端点的双曲线的标准方程是（ ）
| A． | $\frac{{x}^{2}}{84}$-$\frac{{y}^{2}}{16}$=1 | B． | $\frac{{x}^{2}}{16}$-$\frac{{y}^{2}}{84}$=1 | ||
| C． | $\frac{{x}^{2}}{100}$-$\frac{{y}^{2}}{84}$=1 | D． | $\frac{{x}^{2}}{16}$-$\frac{{y}^{2}}{84}$=1或$\frac{{x}^{2}}{100}$-$\frac{{y}^{2}}{84}$=1 |
6．执行如图所示的程序框图，输出结果S=（ ）
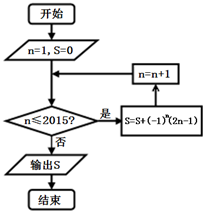
| A． | 2015 | B． | 2016 | C． | -2015 | D． | -2016 |
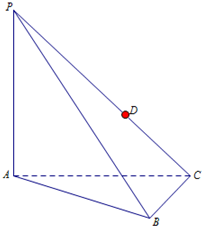如图，在三棱锥P-ABC中，△ABC为等边三角形，AB=2，AP⊥平面ABC，D为PC上的动点．