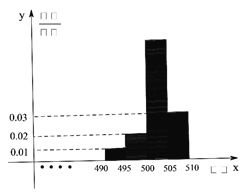ЬтФПФкШн
ЁОЬтФПЁПШчЭМЃЌФГЙЋдАФкгаСНЬѕЕРТЗABЃЌ APЃЌ ЯжМЦЛЎдкAPЩЯбЁдёвЛЕуCЃЌаТНЈЕРТЗBCЃЌВЂАбЁїABCЫљдкЧјгђИФдьГЩТЬЛЏЧјгђЃЌвбжЊЁЯBAC=![]() ЃЌAB=2km.
ЃЌAB=2km.
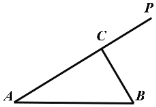
ЃЈ1ЃЉ ШєТЬЛЏЧјгђЁїABCЕФУцЛ§ЮЊ![]() ЃЌЧѓЕРТЗBCЕФГЄЖШЃЛ
ЃЌЧѓЕРТЗBCЕФГЄЖШЃЛ
ЃЈ2ЃЉ ТЬЛЏЧјгђЁїABCУП![]() ЕФИФдьЗбгУгыаТНЈЕРТЗBCУПkmаоНЈЗбгУЖМЪЧНЧЁЯACBЕФКЏЪ§ЃЌЦфжаТЬЛЏЧјгђЁїABCИФдьЗбгУЮЊ
ЕФИФдьЗбгУгыаТНЈЕРТЗBCУПkmаоНЈЗбгУЖМЪЧНЧЁЯACBЕФКЏЪ§ЃЌЦфжаТЬЛЏЧјгђЁїABCИФдьЗбгУЮЊ![]() ЭђдЊ/
ЭђдЊ/![]() ЃЌаТНЈЕРТЗBCаТНЈЗбгУЮЊ
ЃЌаТНЈЕРТЗBCаТНЈЗбгУЮЊ![]() ЭђдЊ/ kmЃЌЩш
ЭђдЊ/ kmЃЌЩш![]() ЃЌФГЙЄГЬЖгГаАќСЫИУЙЋдАЕФТЬЛЏЧјгђИФдьгыаТЕРТЗаоНЈЃЌвбжЊТЬЛЏЧјгђИФдьЗбгыЕРТЗаТНЈЗбгУдНИпЃЌдђЙЄГЬЖгЫљЛёРћШѓвВдНИпЃЌЪдЮЪЕБ
ЃЌФГЙЄГЬЖгГаАќСЫИУЙЋдАЕФТЬЛЏЧјгђИФдьгыаТЕРТЗаоНЈЃЌвбжЊТЬЛЏЧјгђИФдьЗбгыЕРТЗаТНЈЗбгУдНИпЃЌдђЙЄГЬЖгЫљЛёРћШѓвВдНИпЃЌЪдЮЪЕБ![]() ЮЊКЮжЕЪБЃЌИУЙЄГЬЖгЛёЕУзюИпРћШѓ?
ЮЊКЮжЕЪБЃЌИУЙЄГЬЖгЛёЕУзюИпРћШѓ?
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЛЃЈ2ЃЉЕБ
ЃЛЃЈ2ЃЉЕБ![]() ЪБЃЌИУЙЄГЬЖгЛёЕУзюИпРћШѓЃЎ
ЪБЃЌИУЙЄГЬЖгЛёЕУзюИпРћШѓЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнШ§НЧаЮУцЛ§ЙЋЪНЧѓГі![]() ЃЌдйИљОнгрЯвЖЈРэЧѓГі
ЃЌдйИљОнгрЯвЖЈРэЧѓГі![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЩшТЬЛЏЧјгђИФдьЗбгыЕРТЗаТНЈЗбгУжЎКЭЮЊ![]() ЭђдЊЃЌгЩЬтвтЕУ
ЭђдЊЃЌгЩЬтвтЕУ![]() ЃЌгЩе§ЯвЖЈРэПЩЧѓЕУ
ЃЌгЩе§ЯвЖЈРэПЩЧѓЕУ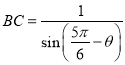 ЃЌ
ЃЌ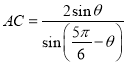 ЃЌИљОнЬтвтНсКЯШ§НЧКуЕШБфЛЛЙЋЪНвдМАИЈжњНЧЙЋЪНПЩЕУ
ЃЌИљОнЬтвтНсКЯШ§НЧКуЕШБфЛЛЙЋЪНвдМАИЈжњНЧЙЋЪНПЩЕУ![]() ЃЌдйНсКЯШ§НЧКЏЪ§ЕФаджЪМДПЩЧѓЕУД№АИЃЎ
ЃЌдйНсКЯШ§НЧКЏЪ§ЕФаджЪМДПЩЧѓЕУД№АИЃЎ
НтЃКЃЈ1ЃЉЁпТЬЛЏЧјгђ![]() ЕФУцЛ§ЮЊ
ЕФУцЛ§ЮЊ![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёп![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
Ёр![]() ЃЌЕУ
ЃЌЕУ![]() ЃЌ
ЃЌ
гЩгрЯвЖЈРэЕУ
![]()
![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
МД![]() ЕФГЄЖШЮЊ
ЕФГЄЖШЮЊ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЩшТЬЛЏЧјгђИФдьЗбгыЕРТЗаТНЈЗбгУжЎКЭЮЊ![]() ЭђдЊЃЌ
ЭђдЊЃЌ
Ёп![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
гЩе§ЯвЖЈРэ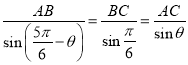 ЕУЃЌ
ЕУЃЌ
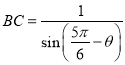 ЃЌ
ЃЌ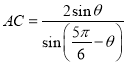 ЃЌ
ЃЌ
дђгЩЬтвтПЩЕУ![]()
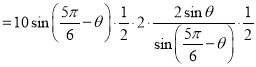
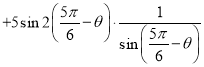
![]()
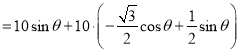
![]()
![]() ЃЌ
ЃЌ
Ёп![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌЕБЧвНіЕБ
ЃЌЕБЧвНіЕБ![]() МД
МД![]() ЪБШЁЕШКХЃЌ
ЪБШЁЕШКХЃЌ
ЁрЕБ![]() ЪБЃЌИУЙЄГЬЖгЛёЕУзюИпРћШѓЃЎ
ЪБЃЌИУЙЄГЬЖгЛёЕУзюИпРћШѓЃЎ

 ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ
ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ
аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИЁОЬтФПЁПЁЖжаЙњКУЩљвєЃЈ![]()
![]()
![]()
![]() ЃЉЁЗЪЧгЩеуНЮРЪгСЊКЯаЧПеДЋУНЦьЯТВгаЧжЦзїЧПСІДђдьЕФДѓаЭРјжОзЈвЕвєРжЦРТлНкФПЃЌгк2012Фъ7дТ13ШедкеуНЮРЪгВЅГі.УПЦкНкФПгаЫФЮЛЕМЪІВЮМг.ЕМЪІБГЖдИшЪжЃЌЕБУПЮЛВЮШќбЁЪжбнГЊЭъжЎЧАгаЕМЪІЮЊЦфзЊЩэЃЌдђИУбЁЪжПЩвдбЁдёМгШыЮЊЦфзЊЩэЕФЕМЪІЕФЭХЖгжаНгЪмжИЕМбЕСЗ.вбжЊФГЦкЁЖжаЙњКУЩљвєЁЗжаЃЌ6ЮЛбЁЪжГЊЭъКѓЃЌЫФЮЛЕМЪІЮЊЦфзЊЩэЕФЧщПіШчЯТБэЫљЪОЃК
ЃЉЁЗЪЧгЩеуНЮРЪгСЊКЯаЧПеДЋУНЦьЯТВгаЧжЦзїЧПСІДђдьЕФДѓаЭРјжОзЈвЕвєРжЦРТлНкФПЃЌгк2012Фъ7дТ13ШедкеуНЮРЪгВЅГі.УПЦкНкФПгаЫФЮЛЕМЪІВЮМг.ЕМЪІБГЖдИшЪжЃЌЕБУПЮЛВЮШќбЁЪжбнГЊЭъжЎЧАгаЕМЪІЮЊЦфзЊЩэЃЌдђИУбЁЪжПЩвдбЁдёМгШыЮЊЦфзЊЩэЕФЕМЪІЕФЭХЖгжаНгЪмжИЕМбЕСЗ.вбжЊФГЦкЁЖжаЙњКУЩљвєЁЗжаЃЌ6ЮЛбЁЪжГЊЭъКѓЃЌЫФЮЛЕМЪІЮЊЦфзЊЩэЕФЧщПіШчЯТБэЫљЪОЃК
ЕМЪІзЊЩэШЫЪ§ЃЈШЫЃЉ | 4 | 3 | 2 | 1 |
ЛёЕУЯргІЕМЪІзЊЩэЕФбЁЪжШЫЪ§ЃЈШЫЃЉ | 1 | 2 | 2 | 1 |
ЯжДгет6ЮЛбЁЪжжаЫцЛњГщШЁСНШЫПМВщЫћУЧбнГЊЭъКѓЕМЪІЕФзЊЩэЧщПі.
ЃЈ1ЃЉЧѓбЁГіЕФСНШЫЕМЪІЮЊЦфзЊЩэЕФШЫЪ§КЭЮЊ4ЕФИХТЪЃЛ
ЃЈ2ЃЉМЧбЁГіЕФ2ШЫЕМЪІЮЊЦфзЊЩэЕФШЫЪ§жЎКЭЮЊ![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФЗжВМСаМАЪ§бЇЦкЭћ
ЕФЗжВМСаМАЪ§бЇЦкЭћ![]() .
.
ЁОЬтФПЁПЫцзХПЦбЇММЪѕЕФЗЩЫйЗЂеЙЃЌЪжЛњЕФЙІФмж№НЅЧПДѓЃЌКмДѓГЬЖШЩЯДњЬцСЫЕчФдЁЂЕчЪгЃЎЮЊСЫСЫНтФГИпаЃбЇЩњЦНОљУПЬьЪЙгУЪжЛњЕФЪБМфЪЧЗёгыадБ№гаЙиЃЌФГЕїВщаЁзщЫцЛњГщШЁСЫ![]() УћФаЩњЁЂ
УћФаЩњЁЂ![]() УћХЎЩњНјааЮЊЦквЛжмЕФИњзйЕїВщЃЌЕїВщНсЙћШчБэЫљЪОЃК
УћХЎЩњНјааЮЊЦквЛжмЕФИњзйЕїВщЃЌЕїВщНсЙћШчБэЫљЪОЃК
ЦНОљУПЬьЪЙгУЪжЛњГЌЙ§ | ЦНОљУПЬьЪЙгУЪжЛњВЛГЌЙ§ | КЯМЦ | |
ФаЩњ |
|
|
|
ХЎЩњ |
|
|
|
КЯМЦ |
|
|
|
ЃЈ1ЃЉФмЗёдкЗИДэЮѓЕФИХТЪВЛГЌЙ§![]() ЕФЧАЬсЯТШЯЮЊбЇЩњЪЙгУЪжЛњЕФЪБМфГЄЖЬгыадБ№гаЙиЃП
ЕФЧАЬсЯТШЯЮЊбЇЩњЪЙгУЪжЛњЕФЪБМфГЄЖЬгыадБ№гаЙиЃП
ЃЈ2ЃЉдкет![]() УћХЎЩњжаЃЌЕїВщаЁзщЗЂЯжЙВга
УћХЎЩњжаЃЌЕїВщаЁзщЗЂЯжЙВга![]() ШЫЪЙгУЙњВњЪжЛњЃЌдкет
ШЫЪЙгУЙњВњЪжЛњЃЌдкет![]() ШЫжаЃЌЦНОљУПЬьЪЙгУЪжЛњВЛГЌЙ§
ШЫжаЃЌЦНОљУПЬьЪЙгУЪжЛњВЛГЌЙ§![]() аЁЪБЕФЙВга
аЁЪБЕФЙВга![]() ШЫЃЎДгЦНОљУПЬьЪЙгУЪжЛњГЌЙ§
ШЫЃЎДгЦНОљУПЬьЪЙгУЪжЛњГЌЙ§![]() аЁЪБЕФХЎЩњжаШЮвтбЁШЁ
аЁЪБЕФХЎЩњжаШЮвтбЁШЁ![]() ШЫЃЌЧѓет
ШЫЃЌЧѓет![]() ШЫжаЪЙгУЗЧЙњВњЪжЛњЕФШЫЪ§
ШЫжаЪЙгУЗЧЙњВњЪжЛњЕФШЫЪ§![]() ЕФЗжВМСаКЭЪ§бЇЦкЭћЃЎ
ЕФЗжВМСаКЭЪ§бЇЦкЭћЃЎ
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ВЮПМЙЋЪНЃК 
![]()
ЁОЬтФПЁПФГЙЋЫОЮЊСЫНтгУЛЇЖдЦфВњЦЗЕФТњвтЖШЃЌДгAЁЂBСНЕиЧјЗжБ№ЫцЛњЕїВщСЫ20ИігУЛЇЃЌЕУЕНгУЛЇЖдВњЦЗЕФТњвтЖШЦРЗжШчЯТЃК
AЕиЧјЃК | 62 | 73 | 81 | 92 | 95 | 85 | 74 | 64 | 53 | 76 |
78 | 86 | 95 | 66 | 97 | 78 | 88 | 82 | 76 | 89 | |
BЕиЧјЃК | 73 | 83 | 62 | 51 | 91 | 46 | 53 | 73 | 64 | 82 |
93 | 48 | 95 | 81 | 74 | 56 | 54 | 76 | 65 | 79 |
ЃЈЂёЃЉИљОнСНзщЪ§ОнЭъГЩСНЕиЧјгУЛЇТњвтЖШЦРЗжЕФОЅвЖЭМЃЌВЂЭЈЙ§ОЅвЖЭМБШНЯСНЕиЧјТњвтЖШЕФЦНОљжЕМАЗжЩЂГЬЖШЃЈВЛвЊЧѓЫуГіОпЬхжЕЃЌИјГіНсТлМДПЩЃЉЃК

ЃЈЂђЃЉИљОнгУЛЇТњвтЖШЦРЗжЃЌНЋгУЛЇЕФТњвтЖШДгЕЭЕНИпЗжЮЊШ§ИіЕШМЖЃК
ТњвтЖШЦРЗж | ЕЭгк70Зж | 70ЗжЕН89Зж | ВЛЕЭгк90Зж |
ТњвтЖШЕШМЖ | ВЛТњвт | Тњвт | ЗЧГЃТњвт |
МЧЪТМўCЃКЁАAЕиЧјгУЛЇЕФТњвтЖШЕШМЖИпгкBЕиЧјгУЛЇЕФТњвтЖШЕШМЖЁБЃЌМйЩшСНЕиЧјгУЛЇЕФЦРМлНсЙћЯрЛЅЖРСЂЃЌИљОнЫљИјЪ§ОнЃЌвдЪТМўЗЂЩњЕФЦЕТЪзїЮЊЯргІЪТМўЗЂЩњЕФИХТЪЃЌЧѓCЕФИХТЪЁЃ