题目内容
【题目】如图,在下列四个正方体中,A,B为正方体的两个顶点,M,N,Q为所在棱的中点,则在这四个正方体中,直线AB与平面MNQ不垂直的是![]()
![]()
A. 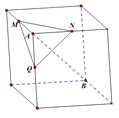 B.
B. 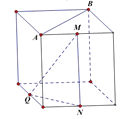
C. 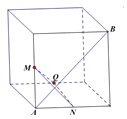 D.
D. 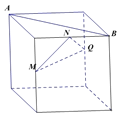
【答案】D
【解析】
由中位线定理和异面直线所成角,以及线面垂直的判定定理,即可得到正确结论.
解:对于A,AB为体对角线,MN,MQ,NQ分别为棱的中点,由中位线定理可得它们平行于所对应的面对角线,连接另一条面对角线,由线面垂直的判定可得AB垂直于MN,MQ,NQ,可得AB垂直于平面MNQ;
对于B,AB为上底面的对角线,显然AB垂直于MN,与AB相对的下底面的面对角线平行,且与直线NQ垂直,可得AB垂直于平面MNQ;
对于C,AB为前面的面对角线,显然AB垂直于MN,QN在下底面且与棱平行,此棱垂直于AB所在的面,即有AB垂直于QN,可得AB垂直于平面MNQ;
对于D,AB为上底面的对角线,MN平行于前面的一条对角线,此对角线与AB所成角为![]() ,
,
则AB不垂直于平面MNQ.
故选:D.

【题目】某品牌手机厂商推出新款的旗舰机型,并在某地区跟踪调查得到这款手机上市时间(第![]() 周)和市场占有率(
周)和市场占有率(![]() )的几组相关数据如下表:
)的几组相关数据如下表:
|
|
|
|
|
|
|
|
|
|
|
|
(1)根据表中的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)根据上述线性回归方程,预测在第几周,该款旗舰机型市场占有率将首次超过![]() (最后结果精确到整数).
(最后结果精确到整数).
参考公式: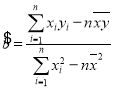 ,
,![]() .
.
【题目】在某区“创文明城区”(简称“创城”)活动中,教委对本区![]() 四所高中学校按各校人数分层抽样,随机抽查了100人,将调查情况进行整理后制成下表:
四所高中学校按各校人数分层抽样,随机抽查了100人,将调查情况进行整理后制成下表:
学校 |
|
|
|
|
抽查人数 | 50 | 15 | 10 | 25 |
“创城”活动中参与的人数 | 40 | 10 | 9 | 15 |
(注:参与率是指:一所学校“创城”活动中参与的人数与被抽查人数的比值)假设每名高中学生是否参与”创城”活动是相互独立的.
(1)若该区共2000名高中学生,估计![]() 学校参与“创城”活动的人数;
学校参与“创城”活动的人数;
(2)在随机抽查的100名高中学生中,随机抽取1名学生,求恰好该生没有参与“创城”活动的概率;
(3)在上表中从![]() 两校没有参与“创城”活动的同学中随机抽取2人,求恰好
两校没有参与“创城”活动的同学中随机抽取2人,求恰好![]() 两校各有1人没有参与“创城”活动的概率是多少?
两校各有1人没有参与“创城”活动的概率是多少?