题目内容
已知数列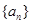 的奇数项是首项为1的等差数列,偶数项是首项为2的等比数列.数列
的奇数项是首项为1的等差数列,偶数项是首项为2的等比数列.数列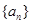 前
前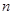 项和为
项和为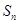 ,且满足
,且满足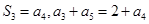
(1)求数列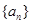 的通项公式;
的通项公式;
(2)求数列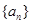 前
前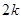 项和
项和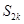 ;
;
(3)在数列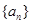 中,是否存在连续的三项
中,是否存在连续的三项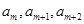 ,按原来的顺序成等差数列?若存在,求出所有满足条件的正整数
,按原来的顺序成等差数列?若存在,求出所有满足条件的正整数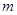 的值;若不存在,说明理由
的值;若不存在,说明理由
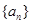 的奇数项是首项为1的等差数列,偶数项是首项为2的等比数列.数列
的奇数项是首项为1的等差数列,偶数项是首项为2的等比数列.数列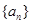 前
前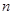 项和为
项和为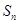 ,且满足
,且满足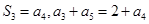
(1)求数列
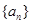 的通项公式;
的通项公式;(2)求数列
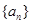 前
前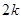 项和
项和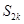 ;
;(3)在数列
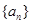 中,是否存在连续的三项
中,是否存在连续的三项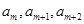 ,按原来的顺序成等差数列?若存在,求出所有满足条件的正整数
,按原来的顺序成等差数列?若存在,求出所有满足条件的正整数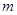 的值;若不存在,说明理由
的值;若不存在,说明理由(1)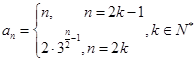 ;(2
;(2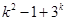 ;(3)存在,详见解析.
;(3)存在,详见解析.
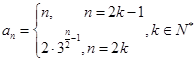 ;(2
;(2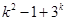 ;(3)存在,详见解析.
;(3)存在,详见解析.试题分析:(1)此类问题一般用等差数列和等比数列的基本量根据题目条件布列方程,解之即可,体现的方程的基本思想,解出等差数列和等比数列后,便可写出数列的通项公式,要注意本题数列的特点,可将其写成分段的形式;(2))在求出等差数列和等比数列的公差和公比后,求得难度已经不大,但要注意分组求和;(3)此类探究性问题,一般先假设存在符合条件的连续三项,然后通过推理,求出则存在,若得到矛盾,则不存在,存在时还要注意求出所有符合条件的解,注意分类讨论思想的应用.
试题解析:(1)设等差数列的公差为
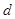 ,等比数列的公比为
,等比数列的公比为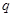 ,
,则
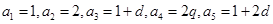
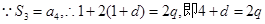
又
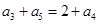 ,
,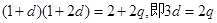 ,解得
,解得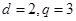
∴对于
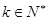 ,有
,有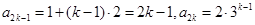
故
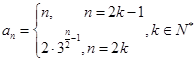 5分
5分(2)由(1)知,在数列
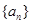 中,前
中,前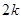 项中所有奇数项的和为
项中所有奇数项的和为 ,所有偶数项的和为
,所有偶数项的和为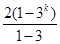 ,所以有
,所以有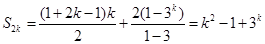 8分
8分(3)在数列
 中,仅存在连续的三项
中,仅存在连续的三项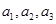 ,按原来的顺序成等差数列,此时正整数
,按原来的顺序成等差数列,此时正整数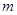 的值为1,下面说明理由 10分
的值为1,下面说明理由 10分若
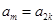 ,则由
,则由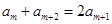 ,得
,得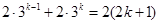
化简得
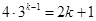 ,此式左边为偶数,右边为奇数,不可能成立 12分
,此式左边为偶数,右边为奇数,不可能成立 12分若
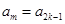 ,则由
,则由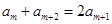 ,得
,得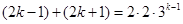
化简得
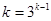 14分
14分令
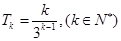 ,则
,则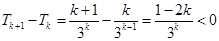
因此,
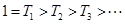 ,故只有
,故只有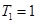 ,此时
,此时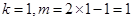
综上,在数列
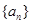 中,仅存在连续的三项
中,仅存在连续的三项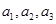 ,按原来的顺序成等差数列,此时正整数
,按原来的顺序成等差数列,此时正整数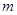 的值为1 16分
的值为1 16分
练习册系列答案
相关题目
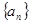 ,
,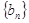 分别为等比,等差数列,数列
分别为等比,等差数列,数列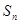 ,且
,且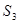 ,
,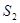 ,
,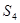 成等差数列,
成等差数列,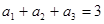 ,数列
,数列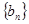 中,
中,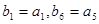 ,
,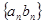 的前n项和为
的前n项和为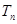 ,求满足不等式
,求满足不等式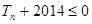 的最小正整数
的最小正整数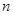 。
。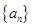 各项为非负实数,前n项和为
各项为非负实数,前n项和为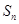 ,且
,且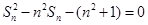
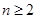 时,求
时,求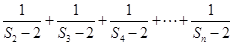 .
.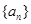 的首项
的首项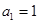 ,公差
,公差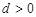 .且
.且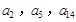 分别是等比数列
分别是等比数列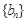 的
的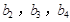 .
. 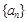 与
与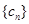 对任意自然数
对任意自然数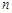 均有
均有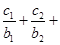 …
…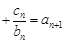 成立,求
成立,求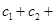 …
…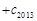 的值.
的值.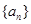 的前
的前 项和为
项和为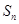 ,若
,若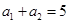 ,
,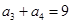 ,则
,则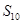 为( )
为( )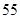
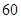
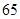
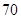
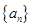 、
、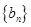 均为等差数列,其前
均为等差数列,其前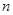 项和分别为
项和分别为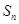 和
和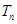 ,若
,若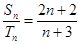 ,则
,则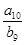 值是( )
值是( )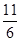
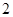
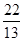
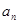 }中,各项都是正数,且
}中,各项都是正数,且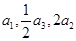 成等差数列,则
成等差数列,则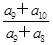 =( )
=( )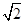
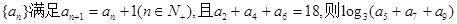 等于( )
等于( )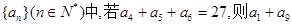 等于( )
等于( )