题目内容
【题目】(2015![]() 福建)如图,AB是圆O的直径,点C是圆O上异于A,B的点,PO垂直于圆O所在的平面,且PO=OB=1.
福建)如图,AB是圆O的直径,点C是圆O上异于A,B的点,PO垂直于圆O所在的平面,且PO=OB=1.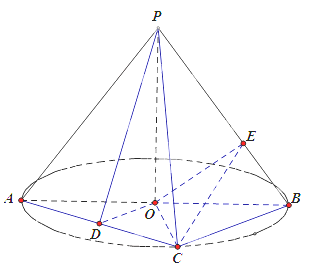
(1)若D为线段AC的中点,求证AC![]() 平面PDO;
平面PDO;
(2)求三棱锥P-ABC体积的最大值;
(3)若BC=![]() ,点E在线段PB上,求CE+OE的最小值.
,点E在线段PB上,求CE+OE的最小值.
【答案】
(1)
详见解析;
(2)
![]() ;
;
(3)
![]() ;
;
【解析】解法一:(1)在![]() AOC中,因为OA=OC,D为AC的中点,所以AC
AOC中,因为OA=OC,D为AC的中点,所以AC![]() OD,又PO垂直于O所在平面,所以PO
OD,又PO垂直于O所在平面,所以PO![]() AC。 因为DO
AC。 因为DO![]() PO=0,所以AC
PO=0,所以AC![]() 平面PDO;
平面PDO;
(2)因为点C是圆O上,所以当CO![]() AB时,C到AB的距离最大,且最大值为1. 又AB=2,所以
AB时,C到AB的距离最大,且最大值为1. 又AB=2,所以![]() ABC的面积的最大值是
ABC的面积的最大值是![]()
![]() =1. 又因为三棱锥P-ABC的高PO=1,故三棱锥P-ABC体积的最大值为
=1. 又因为三棱锥P-ABC的高PO=1,故三棱锥P-ABC体积的最大值为![]() =
=![]()
(3)在![]() POB中,PO=OB=1,
POB中,PO=OB=1,![]() POB=
POB=![]() ,所以PB=
,所以PB=![]() =
=![]() ,同理PC=
,同理PC=![]() ,所以PB=PC=BC,在三棱锥P-ABC,将侧面BCP绕PB旋转至平面BC'P,使之与平面ABP共面,如图所示,当O,E,C'共线时,CE+OE取得最小值。又因为OP=OB,C'P=C'B,所以OC'垂直平分BP,即E为BP中点,从而OC'=OE+EC'=
,所以PB=PC=BC,在三棱锥P-ABC,将侧面BCP绕PB旋转至平面BC'P,使之与平面ABP共面,如图所示,当O,E,C'共线时,CE+OE取得最小值。又因为OP=OB,C'P=C'B,所以OC'垂直平分BP,即E为BP中点,从而OC'=OE+EC'=![]() +
+![]() =
=![]() ,亦即CE+OE的最小值为
,亦即CE+OE的最小值为![]() 。
。
【考点精析】本题主要考查了直线与平面平行的判定的相关知识点,需要掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行才能正确解答此题.

练习册系列答案
相关题目