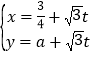题目内容
【题目】已知圆![]() :
:![]() ,直线
,直线![]() :
:![]() .
.
(1)若直线![]() 被圆
被圆![]() 截得的弦长为
截得的弦长为![]() ,求实数
,求实数![]() 的值;
的值;
(2)当![]() 时,由直线
时,由直线![]() 上的动点
上的动点![]() 引圆
引圆![]() 的两条切线,若切点分别为
的两条切线,若切点分别为![]() ,
,![]() ,则在直线
,则在直线![]() 上是否存在一个定点?若存在,求出该定点的坐标;若不存在,请说明理由.
上是否存在一个定点?若存在,求出该定点的坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2) 在直线
;(2) 在直线![]() 上存在一个定点,定点坐标为
上存在一个定点,定点坐标为![]() .
.
【解析】
试题(1)根据直线与圆相交,利用弦长公式即可;(2)根据直线与圆相切的条件,列出方程进行求解判断.
试题解析:(1)圆![]() 的方程可化为
的方程可化为![]() ,
,
故圆心为![]() ,半径
,半径![]() .
.
则圆心![]() 到直线
到直线![]() 的距离为
的距离为![]() .
.
又弦长为![]() ,则
,则![]() ,
,
即![]() ,解得
,解得![]() .
.
(2)当![]() 时,圆
时,圆![]() 的方程为
的方程为![]() ①
①
则圆心为![]() ,半径
,半径![]() ,圆
,圆![]() 与直线
与直线![]() 相离.
相离.
假设在直线![]() 上存在一个定点满足条件,设动点
上存在一个定点满足条件,设动点![]() ,
,
由已知得PA⊥AC,PB⊥BC,
则![]() 在以
在以![]() 为直径的圆
为直径的圆![]() 即
即![]() ②上,
②上,
①—②得,直线![]() 的方程为
的方程为![]() ③
③
又点![]() 在直线
在直线![]() 上,则
上,则![]() ,即
,即![]() ,代入③式
,代入③式
得![]() ,
,
即直线![]() 的方程为
的方程为![]()
因为上式对任意![]() 都成立,故
都成立,故![]() ,得
,得![]() .
.
故在直线![]() 上存在一个定点,定点坐标为
上存在一个定点,定点坐标为![]()

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目