题目内容
(本小题满分10分)选修4—1:几何证明选讲
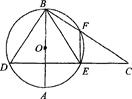
如图所示,已知AB是圆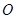 的直径,AC是弦,
的直径,AC是弦, ,垂足为D,AC平分
,垂足为D,AC平分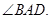
(Ⅰ)求证:直线CE是圆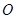 的切线;
的切线;
(Ⅱ)求证: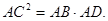
如图所示,已知AB是圆
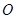 的直径,AC是弦,
的直径,AC是弦, ,垂足为D,AC平分
,垂足为D,AC平分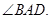

(Ⅰ)求证:直线CE是圆
 的切线;
的切线;(Ⅱ)求证:
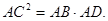
证明: 见解析
本试题主要是考查了平面几何中圆内的性质和三角形的相似性质的运用,以及弦切角定理的综合运用。
(1)利用圆心与直线的连线,垂直于所在直线,得到线与圆相切。
(2)根据题目中的角的关系,和边的关系,得到三角形ABC与三角形ACD相似,从而得到线段相等的证明。
(Ⅰ)连接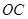 ,因为
,因为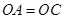 ,所以
,所以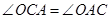 . 2分
. 2分
又因为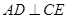 ,所以
,所以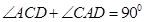 ,
,
又因为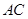 平分
平分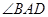 ,所以
,所以 , 4分
, 4分
所以 ,即
,即 ,所以
,所以 是
是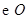 的切线. 6分
的切线. 6分
(Ⅱ)连接 ,因为
,因为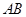 是圆
是圆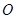 的直径,所以
的直径,所以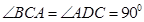 ,
,
因为 , 8分
, 8分
所以△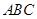 ∽△
∽△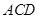 ,所以
,所以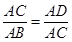 ,即
,即 . 10分
. 10分
(1)利用圆心与直线的连线,垂直于所在直线,得到线与圆相切。
(2)根据题目中的角的关系,和边的关系,得到三角形ABC与三角形ACD相似,从而得到线段相等的证明。
(Ⅰ)连接
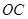 ,因为
,因为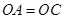 ,所以
,所以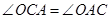 . 2分
. 2分又因为
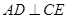 ,所以
,所以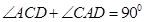 ,
,又因为
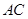 平分
平分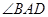 ,所以
,所以 , 4分
, 4分所以
 ,即
,即 ,所以
,所以 是
是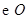 的切线. 6分
的切线. 6分(Ⅱ)连接
 ,因为
,因为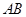 是圆
是圆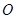 的直径,所以
的直径,所以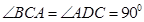 ,
,因为
 , 8分
, 8分所以△
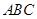 ∽△
∽△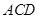 ,所以
,所以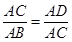 ,即
,即 . 10分
. 10分
练习册系列答案
相关题目
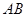 是⊙
是⊙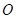 的直径,直线
的直径,直线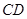 与⊙
与⊙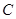 ,
,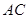 平分
平分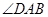 .
.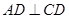 ;
;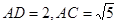 ,求
,求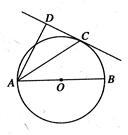
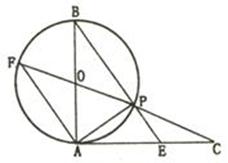
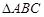 内接于⊙
内接于⊙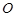 ,
, 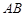 是⊙
是⊙ 是过点
是过点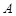 的直线, 且
的直线, 且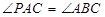 .
.
 交
交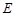 ,
,  ,
,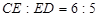 ,
,  , 求
, 求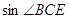 .
.

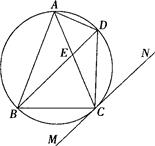
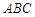 内接于⊙
内接于⊙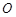 ,
,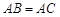 ,直线
,直线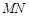 切⊙
切⊙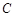 ,弦
,弦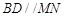 ,
,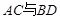 相交于点
相交于点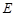 .
.
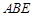 ≌△
≌△ ;
;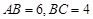 ,求
,求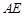 长.
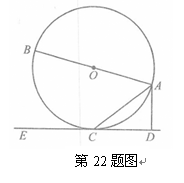
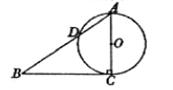
长.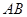 是⊙
是⊙ 的直径,
的直径,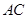 是⊙
是⊙ 的平分线
的平分线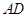 交⊙
交⊙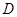 ,过点
,过点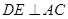 交
交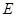 ,
,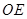 交
交 .若
.若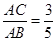 ,则
,则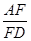 的值为 .
的值为 .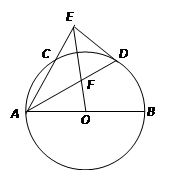
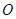 为极点,
为极点,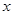 轴的正半轴为极轴,已知点
轴的正半轴为极轴,已知点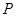 的直角坐标为
的直角坐标为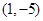 ,点
,点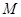 的极坐标为
的极坐标为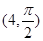 ,若直线
,若直线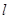 过点
过点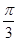 ,圆
,圆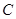 以
以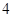 为半径。
为半径。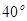 ,则∠DEB___________
,则∠DEB___________