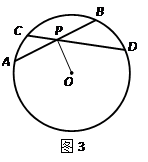题目内容
已知,如图,AB是⊙O的直径,AC切⊙O于点A,AC=AB,CO交⊙O于点P,CO的延长线交⊙O于点F, BP的延长线交AC于点E.
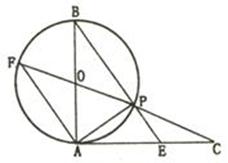
⑴求证:FA∥BE;
⑵求证:

⑴求证:FA∥BE;
⑵求证:

见解析
本试题主要是考查了平面几何中圆与三角形的综合运用。
(1)要证明线线平行,主要是通过证明线线平行的判定定理得到
(2)利用三角形△APC∽△FAC相似,来得到线段成比列的结论。
证明:(1)在⊙O中,∵直径AB与FP交于点O ∴OA=OF
∴∠OAF=∠F ∵∠B=∠F ∴∠OAF="∠B" ∴FA∥BE
(2)∵AC为⊙O的切线,PA是弦 ∴∠PAC=∠F
∵∠C="∠C" ∴△APC∽△FAC ∴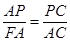
∴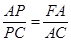 ∵AB=AC ∴
∵AB=AC ∴
(1)要证明线线平行,主要是通过证明线线平行的判定定理得到
(2)利用三角形△APC∽△FAC相似,来得到线段成比列的结论。
证明:(1)在⊙O中,∵直径AB与FP交于点O ∴OA=OF
∴∠OAF=∠F ∵∠B=∠F ∴∠OAF="∠B" ∴FA∥BE
(2)∵AC为⊙O的切线,PA是弦 ∴∠PAC=∠F
∵∠C="∠C" ∴△APC∽△FAC ∴
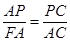
∴
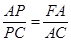 ∵AB=AC ∴
∵AB=AC ∴

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
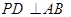 于D,PD与AO的延长线相交于点E,连接CE并延长交圆O于点F,连接AF。
于D,PD与AO的延长线相交于点E,连接CE并延长交圆O于点F,连接AF。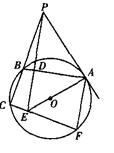
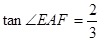 时,求圆O的半径.
时,求圆O的半径. 的直径,AC是弦,
的直径,AC是弦, ,垂足为D,AC平分
,垂足为D,AC平分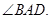
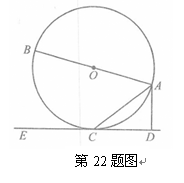
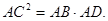
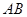 是圆
是圆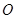 的直径,
的直径,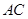 是弦,
是弦,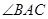 的平分线
的平分线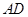 交圆
交圆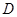 ,
,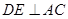 ,交
,交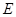 ,
,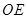 交
交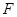 。
。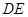 是圆
是圆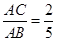 ,求
,求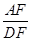 的值。
的值。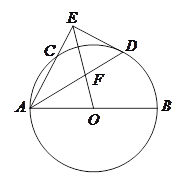
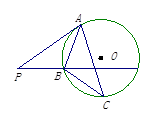
 外一点
外一点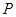 分别作圆的切线和割线交圆于
分别作圆的切线和割线交圆于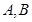 ,且
,且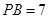 ,
,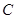 是圆上一点使得
是圆上一点使得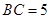 ,
,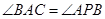 ,则
,则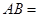 ___________.
___________.
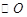 的弦AB上移动,
的弦AB上移动,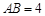 ,连接OD,过点D 作
,连接OD,过点D 作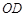 的垂线交
的垂线交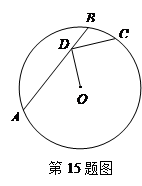
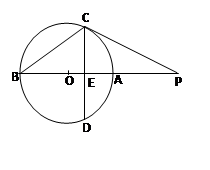
 的半径为
的半径为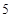
 ,点
,点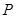 是弦
是弦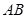 的中点,
的中点,
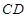 过点
过点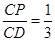 ,则
,则