题目内容
(12分)已知数列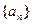 的前n项和为
的前n项和为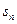 ,
,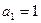 且满足
且满足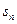 =2
=2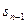 +n (n>1且n
+n (n>1且n ∈
∈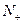 )
)
(1)求数列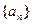 的通项公式和前n项的和
的通项公式和前n项的和
(2)设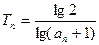 ,求使得不等式
,求使得不等式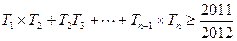 成立的最小正整数n的值
成立的最小正整数n的值
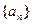 的前n项和为
的前n项和为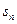 ,
,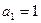 且满足
且满足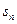 =2
=2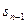 +n (n>1且n
+n (n>1且n ∈
∈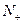 )
)(1)求数列
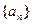 的通项公式和前n项的和
的通项公式和前n项的和(2)设
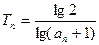 ,求使得不等式
,求使得不等式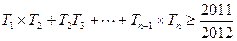 成立的最小正整数n的值
成立的最小正整数n的值解:(1)当n>2时
∵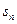 =2
=2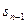 +n
+n
∴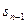 =2
=2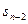 +n-1 ]
+n-1 ]
两式相减得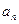 =2
=2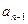 +1
+1
∵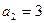 也满足上式
也满足上式
∴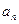 =2
=2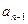 +1 (n>1且n∈
+1 (n>1且n∈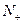 )
)
∴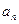 +1=2(
+1=2(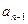 +1)
+1)
又∵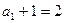 ,∴
,∴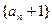 是首项为2,公比为2的等比数列
是首项为2,公比为2的等比数列
∴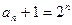 ,∴
,∴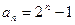 (n∈
(n∈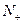 )
)
∴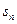 =
=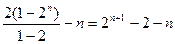 (n∈
(n∈
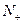 )
)
(2)∵
由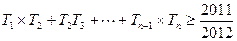 得
得
∴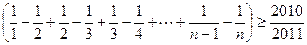
∴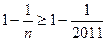 ∴
∴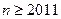 即n的最小值是2011
即n的最小值是2011
∵
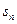 =2
=2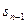 +n
+n∴
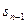 =2
=2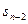 +n-1 ]
+n-1 ]两式相减得
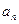 =2
=2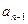 +1
+1 ∵
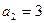 也满足上式
也满足上式∴
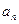 =2
=2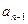 +1 (n>1且n∈
+1 (n>1且n∈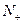 )
)∴
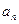 +1=2(
+1=2(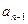 +1)
+1) 又∵
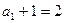 ,∴
,∴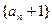 是首项为2,公比为2的等比数列
是首项为2,公比为2的等比数列∴
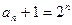 ,∴
,∴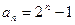 (n∈
(n∈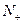 )
)∴
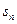 =
=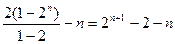 (n∈
(n∈
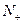 )
)
(2)∵

由
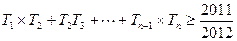 得
得∴
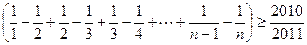
∴
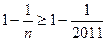 ∴
∴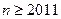 即n的最小值是2011
即n的最小值是2011略

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案
相关题目
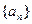 和
和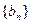 满足:
满足: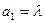 ,
,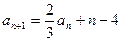 ,
,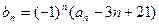 ,其中
,其中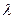 为实数,
为实数,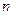 为正整数。
为正整数。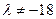 时,数列
时,数列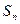 为数列
为数列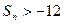 ?若存在,求
?若存在,求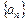 中,
中,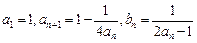 ,其中
,其中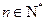 .
.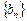 为等差数列;
为等差数列;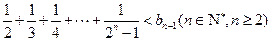
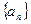 满足:
满足: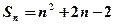 ,其中
,其中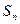 为数列
为数列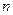 项和.
项和.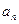 ;
;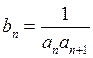 ,求
,求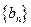 的前n项和Tn..
的前n项和Tn..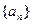 的前n项和为
的前n项和为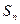 ,并且满足
,并且满足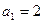 ,
,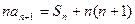 ,
,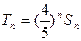 ,问是否存在正整数
,问是否存在正整数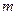 ,对一切正整数
,对一切正整数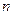 ,总有
,总有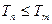 ,若存在,求
,若存在,求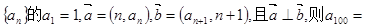 ( )
( )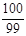
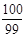
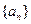 中,
中, 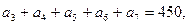 前9项和
前9项和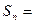 ▲ .
▲ .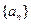 满足
满足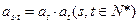 ,且
,且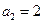 ,则
,则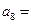 ▲ .
▲ .