题目内容
4．圆x2+y2-2x+4y=0与y-2tx+2t+1=0（t∈R）的位置关系为（ ）| A． | 相离 | B． | 相切 | C． | 相交 | D． | 以上都有可能 |
分析 求出直线系恒过的定点，然后判断点与圆的位置关系，即可得到结果．
解答 解：圆x2+y2-2x+4y=0的圆心（1，-2），半径为：$\sqrt{5}$．
y-2tx+2t+1=0（t∈R），
直线恒过（1，-1）．
因为$\sqrt{{（1-1）}^{2}+{（-2+1）}^{2}}$=1$＜\sqrt{5}$．
所以直线系恒过圆内的点，所以直线与圆相交．
故选：C．
点评 本题考查直线与圆的位置关系的应用，考查计算能力．
练习册系列答案
相关题目
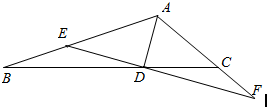已知△ABC中，AB=2，AC=1，∠BAC=120°，AD为角平分线．
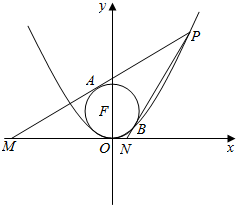（文科）如图，已知抛物线C：y=$\frac{1}{4}$x2，点P（x0，y0）为抛物线上一点，y0∈[3，5]，圆F方程为x2+（y-1）2=1，过点P作圆F的两条切线PA，PB分别交x轴于点M，N，切点分别为A，B．