Question

【题目】已知函数.

（Ⅰ）当时，求证： ，并指出等号成立的条件；

（Ⅱ）求证：对任意实数，总存在实数，有.

Answer 1

【答案】(Ⅰ)证明见解析；(Ⅱ)证明见解析

【解析】试题分析：

(Ⅰ)构造新函数 ，利用导函数研究函数的单调性可得，据此即可证得.

(Ⅱ)原问题等价于.然后分类讨论当时和当时的情况即可证得题中的结论.

试题解析：

（Ⅰ）设 .

∵，

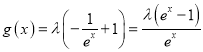∴当时， ，故递增；当时， ，故递减.

因此， ，即，当且仅当时等号成立.

（Ⅱ）解法一：“存在实数，有”等价于.

注意到.∵，

∴当时， ，故在上单调递增，从而成立；

当时，令，得，∴在上递减，在上递增

若，即时， 在上递增，故成立；

若，即时， 在上递增，故成立；

若，即时， 在上递减，在上递增，

故成立.

综上所述，对任意实数，总存在实数，有.

解法二：①当时， 在区间上递增，则，

②当时，由（Ⅰ）可知；

③当时，由（Ⅰ）可知

综上，对任意实数，总存在实数，有.