题目内容
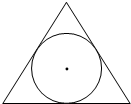如图，在边长为2的正三角形内随机取一个点A，则点A在此正三角形的内切圆的内部的概率为（ ）A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点：几何概型
专题：计算题,概率与统计
分析：点A在此正三角形的内切圆的内部的概率就是内切圆的面积与正三角形面积的比．
解答：
解：∵如图所示的正三角形，
∴∠CAB=60°，
设三角形的边长是a，
∴AB=
a，
∵⊙O是内切圆，
∴∠OAB=30°，∠OBA=90°，
∴BO=tan30°AB=
a，
则正三角形的面积是
a2，而圆的半径是
a，面积是
a2，
因此概率是
a2÷
a2=
．
故选：A．
解：∵如图所示的正三角形，∴∠CAB=60°，
设三角形的边长是a，
∴AB=
| 1 |
| 2 |
∵⊙O是内切圆，
∴∠OAB=30°，∠OBA=90°，
∴BO=tan30°AB=
| ||
| 6 |
则正三角形的面积是
| ||
| 4 |
| ||
| 6 |
| π |
| 12 |
因此概率是
| π |
| 12 |
| ||
| 4 |
| ||
| 9 |
故选：A．
点评：本题主要考查几何概型中的面积类型，基本方法是：分别求得构成事件A的区域面积和试验的全部结果所构成的区域面积，两者求比值，即为概率．
练习册系列答案
开心练习课课练与单元检测系列答案
相关题目
圆O1：x2+y2-2x=0和圆O2：x2+y2-4y=0的公切线条数（ ）
| A、1条 | B、2条 | C、3条 | D、4条 |
阅读如图所示的程序框图，运行相应的程序，若输入m=2014，n=6，则输出n的值为（ ）
| A、2014 | B、4 | C、3 | D、2 |
一个盒子里装有标号为1，2，3，4，5的5张标签，随机地选取两张标签，若标签的选取是有放回的，则两张标签上的数字为相邻整数的概率是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
在区间[-π，π]上随机取一个数x，则事件：“cosx≥0”的概率为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
已知a是第三象限角，且tana=
，则sina等于（ ）
| 1 |
| 2 |
A、-
| ||||
B、
| ||||
C、-
| ||||
D、
|
在△ABC中，若
•
＞|
|2，则有（ ）
| AC |
| AB |
| AC |
A、|
| ||||
B、|
| ||||
C、|
| ||||
D、|
|
若a＞b＞0，c＜d＜0，则一定有（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|