题目内容
在区间[-π,π]上随机取一个数x,则事件:“cosx≥0”的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:几何概型
专题:概率与统计
分析:解:求出cosx≥0的等价条件,利用几何概型的概率公式即可得到结论.
解答:解:在[-π,π]由cosx≥0得-
≤x≤
,
则由几何概型的概率公式可得:“cosx≥0”的概率P=
=
=
,
故选:D
| π |
| 2 |
| π |
| 2 |
则由几何概型的概率公式可得:“cosx≥0”的概率P=
| ||||
| π-(-π) |
| π |
| 2π |
| 1 |
| 2 |
故选:D
点评:本题主要考查几何概型的概率计算,根据三角函数的性质是解决本题的关键.

练习册系列答案
相关题目
直线x-
y=0被圆x2+y2-8x+4=0截得的弦长为( )
| 3 |
A、2
| ||
| B、4 | ||
C、4
| ||
D、4
|
某程序框图如图所示,当程序运行后,输出T的值是( )


| A、30 | B、31 | C、55 | D、56 |
将区间[0,1]内的随机数转化为[-2,6]内的均匀随机数,需实施的变换为( )
| A、a=a1*8 | B、a=a1*8+2 | C、a=a1*8-2 | D、a=a1*6 |
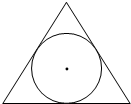 如图,在边长为2的正三角形内随机取一个点A,则点A在此正三角形的内切圆的内部的概率为( )
如图,在边长为2的正三角形内随机取一个点A,则点A在此正三角形的内切圆的内部的概率为( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
设角α的终边与单位圆相交于点P(
,-
),则sinα-cosα的值是( )
| 3 |
| 5 |
| 4 |
| 5 |
A、-
| ||
B、-
| ||
C、
| ||
D、
|
已知向量
=(-1,5),
=(2,3),则向量2
+
的坐标为( )
| a |
| b |
| a |
| b |
| A、(1,3) |
| B、(2,4) |
| C、(5,4) |
| D、(0,13) |
等差数列{an}的前n项和为Sn,已知1≤S2≤2,3≤S4≤5,则S6的取值范围是( )
| A、[3,12] | B、[4,12] | C、[5,11] | D、[5,8] |