题目内容
已知a是第三象限角,且tana=
,则sina等于( )
| 1 |
| 2 |
A、-
| ||||
B、
| ||||
C、-
| ||||
D、
|
考点:同角三角函数基本关系的运用
专题:三角函数的求值
分析:由α为第三象限角,且tanα的值,利用同角三角函数间基本关系求出cos2α的值,即可确定出sinα的值.
解答:解:∵α是第三象限角,且tanα=
,
∴cos2α=
=
,
则sinα=-
=-
.
故选:C.
| 1 |
| 2 |
∴cos2α=
| 1 |
| 1+tan2α |
| 4 |
| 5 |
则sinα=-
| 1-cos2α |
| ||
| 5 |
故选:C.
点评:此题考查了同角三角函数基本关系的运用,熟练掌握基本关系是解本题的关键.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案
相关题目
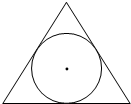 如图,在边长为2的正三角形内随机取一个点A,则点A在此正三角形的内切圆的内部的概率为( )
如图,在边长为2的正三角形内随机取一个点A,则点A在此正三角形的内切圆的内部的概率为( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
设角α的终边与单位圆相交于点P(
,-
),则sinα-cosα的值是( )
| 3 |
| 5 |
| 4 |
| 5 |
A、-
| ||
B、-
| ||
C、
| ||
D、
|
已知0°<2α<90°,90°<β<180°,a=(sinα)cosβ,b=(cosα)sinβ,c=(cosα)cosβ,则a、b、c的大小关系是( )
| A、a>c>b | B、a<b<c | C、b>a>c | D、c>a>b |
已知向量
=(-1,5),
=(2,3),则向量2
+
的坐标为( )
| a |
| b |
| a |
| b |
| A、(1,3) |
| B、(2,4) |
| C、(5,4) |
| D、(0,13) |
如果sin2θ+2sinθ>cos2θ+2cosθ,且θ∈(0,2π),那么角θ的取值范围是( )
A、(0,
| ||||
B、(
| ||||
C、(
| ||||
D、(
|
原命题为“若
<an,n∈N+,则{an}为递减数列”,关于其逆命题,否命题,逆否命题真假性的判断依次如下,正确的是( )
| an+an+1 |
| 2 |
| A、真、真、真 |
| B、假、假、真 |
| C、真、真、假 |
| D、假、假、假 |