题目内容
在△ABC中，若
•
＞|
|2，则有（ ）
| AC |
| AB |
| AC |
A、|
| ||||
B、|
| ||||
C、|
| ||||
D、|
|
考点：平面向量数量积的运算
专题：平面向量及应用
分析：利用向量的投影，判断出角C是钝角，问题得以解决．
解答：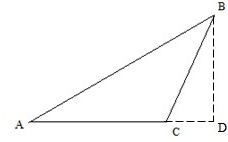
解：∵
•
＞|
|2，
∴||
||
|cos∠A＞|
|2，
∴|
|cos∠A＞|
|，
∵|
|cos∠A是
在
上的投影，
如图所示，
∴|
|cos∠A=|
|＞|
|，
∴必须C为钝角时才能满足|
|cos∠A＞|
|，
根据大角对大边得|
|最长，
故选：D．
解：∵| AC |
| AB |
| AC |
∴||
| AC |
| AB |
| AC |
∴|
| AB |
| AC |
∵|
| AB |
| AB |
| AC |
如图所示，
∴|
| AB |
| AD |
| AC |
∴必须C为钝角时才能满足|
| AB |
| AC |
根据大角对大边得|
| AB |
故选：D．
点评：本题考查了向量的数量积和向量的投影问题，关键是求出角C是钝角．
练习册系列答案
相关题目
运行如图的程序框图，若输出的结果是s=1320，则判断框中可填入（ ）
| A、k≤10？ | B、k＜10？ | C、k＜9？ | D、k≤8？ |
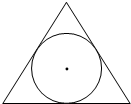如图，在边长为2的正三角形内随机取一个点A，则点A在此正三角形的内切圆的内部的概率为（ ）A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知0°＜2α＜90°，90°＜β＜180°，a=（sinα）cosβ，b=（cosα）sinβ，c=（cosα）cosβ，则a、b、c的大小关系是（ ）
| A、a＞c＞b | B、a＜b＜c | C、b＞a＞c | D、c＞a＞b |
已知向量
=（-1，5），
=（2，3），则向量2
+
的坐标为（ ）
| a |
| b |
| a |
| b |
| A、（1，3） |
| B、（2，4） |
| C、（5，4） |
| D、（0，13） |
已知
=（2，1），
=（2，-3），若k
+
与
-2
垂直，则k=（ ）
| a |
| b |
| a |
| b |
| a |
| b |
| A、2 | ||
B、
| ||
C、
| ||
D、
|
如果sin2θ+2sinθ＞cos2θ+2cosθ，且θ∈（0，2π），那么角θ的取值范围是（ ）
A、（0，
| ||||
B、（
| ||||
C、（
| ||||
D、（
|