题目内容
若1<α<3,-4<β<2,则
α-β的取值范围是 .
| 1 | 2 |
考点:弧度制的应用
专题:不等式的解法及应用
分析:由已知中1<α<3,-4<β<2,先求出
α和-β的取值范围,进而根据不等式的同号可加性,得到
α-β的取值范围.
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:∵1<α<3,
∴
<
α<
…①,
∵-4<β<2,
∴-2<-β<4…②,
由①②结合不等式的基本性质可得:
-
<
a-β<
,
即
α-β的取值范围是(-
,
),
故答案为:(-
,
)
∴
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
∵-4<β<2,
∴-2<-β<4…②,
由①②结合不等式的基本性质可得:
-
| 3 |
| 2 |
| 1 |
| 2 |
| 11 |
| 2 |
即
| 1 |
| 2 |
| 3 |
| 2 |
| 11 |
| 2 |
故答案为:(-
| 3 |
| 2 |
| 11 |
| 2 |
点评:本题考查的知识点是不等式的基本性质,熟练掌握不等式的基本性质,是解答的关键.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
一种电子小型娱乐游戏的主界面是半径为r的一个圆,点击圆周上点A后该点在圆周上随机转动,最终落点为B,当线段AB的长不小于
r时自动播放音乐,则一次转动能播放出音乐的概率为( )
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
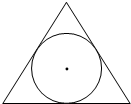 如图,在边长为2的正三角形内随机取一个点A,则点A在此正三角形的内切圆的内部的概率为( )
如图,在边长为2的正三角形内随机取一个点A,则点A在此正三角形的内切圆的内部的概率为( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知0°<2α<90°,90°<β<180°,a=(sinα)cosβ,b=(cosα)sinβ,c=(cosα)cosβ,则a、b、c的大小关系是( )
| A、a>c>b | B、a<b<c | C、b>a>c | D、c>a>b |
已知
=(2,1),
=(2,-3),若k
+
与
-2
垂直,则k=( )
| a |
| b |
| a |
| b |
| a |
| b |
| A、2 | ||
B、
| ||
C、
| ||
D、
|
已知变量x,y满足约束条件
,则z=x2+y2+2的最大值( )
|
| A、15 | B、17 | C、18 | D、19 |
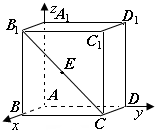 如图,已知正方体ABCD-A1B1C1D1棱长为2,E是线段B1C的中点,分别以AB、AD、AA1为x、y、z轴建立如图所示的空间直角坐标系A-xyz,点E的坐标是
如图,已知正方体ABCD-A1B1C1D1棱长为2,E是线段B1C的中点,分别以AB、AD、AA1为x、y、z轴建立如图所示的空间直角坐标系A-xyz,点E的坐标是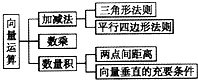 如图是向量运算的知识结构图,如果要加入“向量共线的充要条件”,则应该是在
如图是向量运算的知识结构图,如果要加入“向量共线的充要条件”,则应该是在