题目内容
10.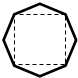 某班设计了一个八边形的班徽(如图),它由腰长为1,顶角为α的四个等腰三角形,及其底边构成的正方形所组成,则该八边形的面积的最大值为$2\sqrt{2}+2$.
某班设计了一个八边形的班徽(如图),它由腰长为1,顶角为α的四个等腰三角形,及其底边构成的正方形所组成,则该八边形的面积的最大值为$2\sqrt{2}+2$.
分析 根据正弦定理可先求出4个三角形的面积,再由三角面积公式可求出正方形的边长进而得到面积,最后得到答案.
解答 解:由正弦定理可得4个等腰三角形的面积和为:4×$\frac{1}{2}$×1×1×sinα=2sinα,
由余弦定理可得正方形边长为:$\sqrt{1+1-2×1×1×cosα}$=$\sqrt{2-2cosα}$,
故正方形面积为:2-2cosα,
所以所求八边形的面积为:2sinα-2cosα+2=2$\sqrt{2}$sin(α-$\frac{π}{4}$)+2,
所以该八边形的面积的最大值为$2\sqrt{2}+2$.
故答案为:$2\sqrt{2}+2$.
点评 本题考查了三角面积公式的应用和余弦定理的应用.正、余弦定理是考查解三角形的重点,是必考内容.

练习册系列答案
 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
2.已知函数f(x)=$\frac{1}{2}$mx2+lnx-2x在定义域内是增函数,则实数m的取值范围为( )
| A. | (-∞,-2] | B. | (-∞,-1] | C. | [0,+∞) | D. | [1,+∞) |
19.若集合A={1,m2},B={3,4},则“m=2”是“A∩B={4}”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |