题目内容
已知圆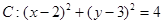 ,直线
,直线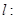
 ,
,
(1)求证:直线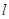 与圆
与圆 恒相交;
恒相交;
(2)当 时,过圆
时,过圆 上点
上点 作圆的切线
作圆的切线 交直线
交直线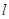 于
于 点,
点, 为圆
为圆 上的动点,求
上的动点,求 的取值范围;
的取值范围;
(1)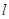 恒过两直线
恒过两直线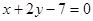 及
及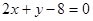 的交点
的交点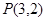 ;(2)
;(2)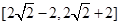 。
。
解析试题分析:(1)证明:由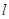 得方程得
得方程得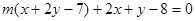 ,
,
故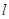 恒过两直线
恒过两直线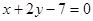 及
及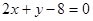 的交点
的交点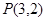 ,
,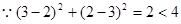 ,即点
,即点 在圆
在圆 内部,
内部, 直线
直线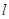 与圆
与圆 恒相交。
恒相交。
(2)由题知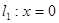
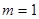 时,
时,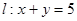
所以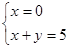

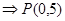 ,而
,而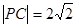 ,所以
,所以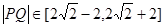
考点:直线系方程;直线与圆的位置关系。
点评:定点直线系:若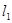 :
: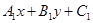 =0和
=0和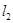 :
: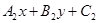 =0相交,则过
=0相交,则过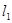 与
与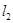 交点的直线系为
交点的直线系为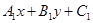 +λ
+λ =0。
=0。

练习册系列答案
相关题目
 关于直线
关于直线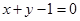 对称,圆心
对称,圆心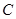 在第二象限,半径为
在第二象限,半径为 .
. 与圆
与圆 轴、
轴、 轴上的截距相等?若存在,求直线的方程;若不存在,说明理由。
轴上的截距相等?若存在,求直线的方程;若不存在,说明理由。 ,过动点P分别作圆O1.圆O2的切线PM、PN(M.N分别为切点),使得
,过动点P分别作圆O1.圆O2的切线PM、PN(M.N分别为切点),使得 试建立适当的坐标系,并求动点P的轨迹方程
试建立适当的坐标系,并求动点P的轨迹方程
 的圆心
的圆心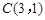 ,被
,被 轴截得的弦长为
轴截得的弦长为 .
. 交于
交于 ,
, 两点,且
两点,且 ,求
,求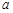 的值.
的值. :
: ,圆
,圆 方程为
方程为
 的值
的值 为圆心的圆与直线
为圆心的圆与直线 相切.过点
相切.过点 的动直线
的动直线 与圆
与圆 相交于
相交于 两点,
两点, 是
是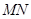 的中点.
的中点.
 时,求直线
时,求直线 和
和 .
. 上,求圆的方程。
上,求圆的方程。 ,
, 内接于此圆,
内接于此圆, 点的坐标
点的坐标 ,
, 为坐标原点.
为坐标原点. ,求直线
,求直线 的方程;
的方程;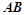 与直线
与直线 的倾斜角互补,求证:直线
的倾斜角互补,求证:直线