题目内容
(本大题10分)求圆心在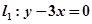 上,与
上,与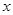 轴相切,且被直线
轴相切,且被直线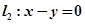 截得弦长为
截得弦长为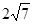 的圆的方程.
的圆的方程.
 或
或 。
。
解析试题分析:根据圆心在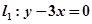 上,可设圆心坐标为(
上,可设圆心坐标为( ),再根据它与
),再根据它与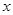 轴相切,得
轴相切,得 .
.
圆心到直线的距离等于 ,根据弦长公式可得
,根据弦长公式可得 ,从而求出a的值,写出圆的标准方程.
,从而求出a的值,写出圆的标准方程.
由已知设圆心为( )--------1分
)--------1分
与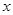 轴相切则
轴相切则 ---------2分
---------2分
圆心到直线的距离 ----------3分
----------3分
弦长为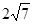 得:
得: -------6分
-------6分
解得 ---------7分
---------7分
圆心为(1,3)或(-1,-3), -----------8分
-----------8分
圆的方程为 ---------9分
---------9分
或 ----------10.
----------10.
考点:圆的标准方程.
点评:解本小题要利用点到直线的距离公式及圆的弦长公式:
点到直线的距离公式: 则
则 .
.
圆的弦长公式:弦长 .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
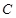 经过
经过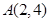 、
、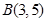 两点,且圆心C在直线
两点,且圆心C在直线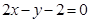 上.
上.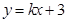 与圆
与圆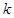 的取值范围.
的取值范围. 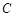 的圆心
的圆心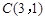 ,被
,被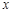 轴截得的弦长为
轴截得的弦长为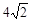 .
.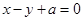 交于
交于 ,
,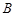 两点,且
两点,且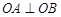 ,求
,求 的值.
的值.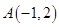 为圆心的圆与直线
为圆心的圆与直线 相切.过点
相切.过点 的动直线
的动直线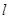 与圆
与圆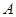 相交于
相交于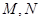 两点,
两点,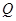 是
是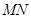 的中点.
的中点.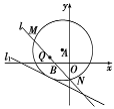
 时,求直线
时,求直线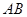 是⊙
是⊙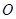 的直径,
的直径,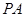 垂直于⊙
垂直于⊙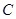 是圆周上不同于
是圆周上不同于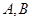 的一动点.
的一动点.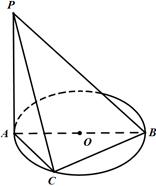
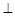 面PBC;
面PBC; ,则当直线
,则当直线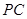 与平面
与平面 所成角正切值为
所成角正切值为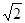 时,求直线
时,求直线 所成角的正弦值.
所成角的正弦值.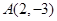 和
和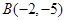 .
.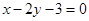 上,求圆的方程。
上,求圆的方程。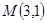 ,直线
,直线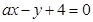 及圆
及圆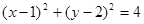 .
.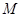 点的圆的切线方程;
点的圆的切线方程;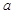 的值;
的值;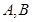 两点,且弦
两点,且弦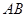 的长为
的长为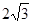 ,求
,求 N(1,0)的距离的比为。
N(1,0)的距离的比为。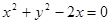 相外切,并且与直线
相外切,并且与直线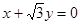 相切于点
相切于点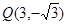 ,求圆C的
,求圆C的