题目内容
10.函数f(x)=(1+x-$\frac{x^2}{2}$+$\frac{x^3}{3}$-$\frac{x^4}{4}$+…-$\frac{{{x^{2012}}}}{2012}$+$\frac{{{x^{2013}}}}{2013}$-$\frac{{{x^{2014}}}}{2014}$+$\frac{{{x^{2015}}}}{2015}}$)cos2x在区间[-3,3]上零点的个数为( )| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
分析 令g(x)=1+x-$\frac{x^2}{2}$+$\frac{x^3}{3}$-$\frac{x^4}{4}$+…-$\frac{{{x^{2012}}}}{2012}$+$\frac{{{x^{2013}}}}{2013}$-$\frac{{{x^{2014}}}}{2014}$+$\frac{{{x^{2015}}}}{2015}}$,由其导函数判断其在[-3,3]上为单调函数,且有一个零点,而y=cos2x在区间[-3,3]上有4个零点,则答案可求.
解答 解:设g(x)=1+x-$\frac{x^2}{2}$+$\frac{x^3}{3}$-$\frac{x^4}{4}$+…-$\frac{{{x^{2012}}}}{2012}$+$\frac{{{x^{2013}}}}{2013}$-$\frac{{{x^{2014}}}}{2014}$+$\frac{{{x^{2015}}}}{2015}}$,
则g′(x)=1-x+x2-x3+…+x2014=$\frac{1+{x}^{2015}}{1+x}$,
在区间[-3,3]上,$\frac{1+{x}^{2015}}{1+x}$>0,故函数g(x)在[-3,3]上是增函数,
由于g(-3)式子中右边x的指数为偶次项前为负,奇数项前为正,结果必负,即g(-3)<0,
且g(3)=1+3+(-$\frac{x^2}{2}$+$\frac{x^3}{3}$)+(-$\frac{x^4}{4}$+$\frac{{x}^{5}}{5}$)+…+(-$\frac{{{x^{2012}}}}{2012}$+$\frac{{{x^{2013}}}}{2013}$)+(-$\frac{{{x^{2014}}}}{2014}$+$\frac{{{x^{2015}}}}{2015}}$)>0,
故在[-3,3]上函数g(x)有且只有一个零点.
又y=cos2x在区间[-3,3]上有四个零点,且与上述零点不重复,
∴函数f(x)=(1+x-$\frac{x^2}{2}$+$\frac{x^3}{3}$-$\frac{x^4}{4}$+…-$\frac{{{x^{2012}}}}{2012}$+$\frac{{{x^{2013}}}}{2013}$-$\frac{{{x^{2014}}}}{2014}$+$\frac{{{x^{2015}}}}{2015}}$)cos2x在区间[-3,3]上的零点的个数为1+4=5.
故选C.
点评 本题考查基本初等函数的导函数的求法,考查了函数零点的判断,是中档题.

 通城学典默写能手系列答案
通城学典默写能手系列答案| A. | 若m⊥α,m⊥β,则α∥β | B. | 若m⊥α,n⊥α,则m∥n | C. | 若α∥γ,β∥γ,则α∥β | D. | 若α⊥γ,β⊥γ,则α∥β |
| A. | $f({-\frac{1}{2}})<f({\frac{3}{4}})<f({\frac{2}{3}})$ | B. | $f({-\frac{1}{2}})<f({\frac{2}{3}})<f({\frac{3}{4}})$ | C. | $f({\frac{3}{4}})<f({\frac{2}{3}})<f({-\frac{1}{2}})$ | D. | $f({\frac{2}{3}})<f({-\frac{1}{2}})<f({\frac{3}{4}})$ |
| A. | E,F,G,H四点不共面 | B. | EFGH是梯形 | ||
| C. | EG⊥FH | D. | EFGH是矩形 |
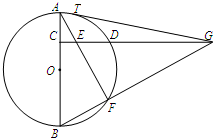 如图,C是⊙O的直径AB上一点,CD⊥AB,与⊙O相交于点D,与弦AF交于点E,与BF的延长线交于点G,GT与⊙O相切于点T.
如图,C是⊙O的直径AB上一点,CD⊥AB,与⊙O相交于点D,与弦AF交于点E,与BF的延长线交于点G,GT与⊙O相切于点T. 如图,已知AB为半圆O的直径,C为圆弧上一点,过点C作半圆的切线CF,过点A作CF的垂线,垂足为D,AD交半圆于点E,连结EC,BC,AC.
如图,已知AB为半圆O的直径,C为圆弧上一点,过点C作半圆的切线CF,过点A作CF的垂线,垂足为D,AD交半圆于点E,连结EC,BC,AC.