题目内容
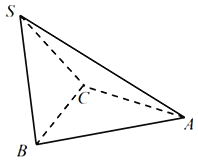
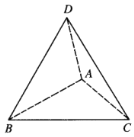
【题目】如图,![]() 中,
中,![]() ,
,![]() 为线段
为线段![]() 上一点,且
上一点,且![]() ,让
,让![]() 绕直线
绕直线![]() 翻折到
翻折到![]() 且使
且使![]() .
.
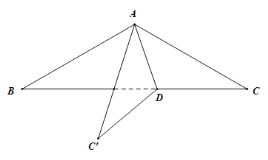
(Ⅰ)在线段![]() 上是否存在一点
上是否存在一点![]() ,使平面
,使平面![]() 平面
平面![]() ?请证明你的结论;
?请证明你的结论;
(Ⅱ)求直线![]() 与平面
与平面![]() 所成的角.
所成的角.
【答案】(Ⅰ)存在,见解析(Ⅱ)![]()
【解析】
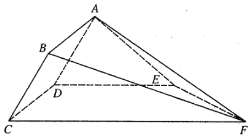
(Ⅰ)取BC中点为E,由题意知![]() ,再由
,再由![]() ,得
,得![]() 平面
平面![]() ,从而平面
,从而平面![]() 平面
平面![]() ;
;
(Ⅱ)在平面![]() 中,过
中,过![]() 作
作![]() 交AE 于点H,连接HD,由
交AE 于点H,连接HD,由![]() 平面
平面![]() ,得
,得![]() 为直线
为直线![]() 与平面
与平面![]() 所成的角,由此能求出直线
所成的角,由此能求出直线![]() 与平面
与平面![]() 所成的角的大小.
所成的角的大小.
(Ⅰ)在线段![]() 上存在中点
上存在中点![]() ,使平面
,使平面![]() 平面
平面![]() ,
,
证明如下:取![]() 的中点为
的中点为![]() ,连接
,连接![]() ,
,
由题意知![]() ,
,
又因为![]() ,
,
所以![]() 平面
平面![]() ,
,
因为![]() 在平面
在平面![]() 内,
内,
所以平面![]() 平面
平面![]() .
.

(Ⅱ)在平面![]() 中,过点
中,过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,连接
,连接![]() .
.
由(Ⅰ)知,![]() 平面
平面![]() ,
,
所以![]() 为直线
为直线![]() 与平面
与平面![]() 所成的角.
所成的角.
由题意知![]() ,
,
所以在![]() 中,
中,![]() ,
,
所以在![]() 中,由余弦定理得
中,由余弦定理得 ,
,
所以![]() ,
,
所以![]() ,
,
所以![]() ,所以
,所以![]() ,
,
即直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() .
.

练习册系列答案
相关题目