Question

【题目】选修4-4：坐标系与参数方程

在直角坐标系中，以坐标原点为极点，轴的非负半轴为极轴建立极坐标系．已知点的极坐标为，曲线 的参数方程为（为参数）．

（1）直线过且与曲线相切，求直线的极坐标方程；

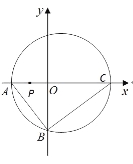
（2）点与点关于轴对称，求曲线上的点到点的距离的取值范围．

Answer 1

【答案】（1）或；（2）．

【解析】

试题分析：对于问题（1）可以先求出点的直角坐标以及曲线的普通方程，利用直线过且与曲线相切，即可求直线的极坐标方程；对问题（2）可以先根据点与点关于轴对称，求出点的坐标，再求出点到圆心的距离，从而可求曲线上的点到点的距离的取值范围．

试题解析：（1）由题意得点的直角坐标为，曲线的一般方程为

设直线的方程为，即，

∵直线过且与曲线 相切，∴，

即，解得，

∴直线的极坐标方程为或，

（2）∵点与点关于轴对称，∴点的直角坐标为，

则点到圆心的距离为，

曲线上的点到点的距离的最小值为，最大值为，

曲线 上的点到点的距离的取值范围为