题目内容
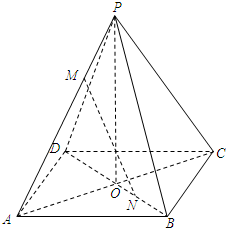 如图,正四棱锥P-ABCD中,PA=AB,点M,N分别在PA,BD上,且
如图,正四棱锥P-ABCD中,PA=AB,点M,N分别在PA,BD上,且| PM |
| PA |
| BN |
| BD |
| 1 |
| 3 |
(Ⅰ)求异面直线MN与AD所成角;
(Ⅱ)求证:MN∥平面PBC;
(Ⅲ)求MN与平面PAB所成角的正弦值.
分析:题干错误:
=
=
,应该是:
=
=
,请给修改,谢谢
(Ⅰ)设AC与BD的交点为O,AB=PA=2.如图所示,建立空间直角坐标系,求得A、B、C、D的坐标.求得
=
+
=
+
、
=
的
坐标,可得
和
的坐标,根据
•
=0,可得异面直线MN与AD所成角的值.
(Ⅱ)设平面PBC的法向量为
=(a,b,c),由
•
=0,
•
=0,求得
的坐标,根据
•
=0,证得MN∥平面PBC.
(Ⅲ)设平面PAB的法向量为
=(x,y,z),由
•
=0
•
=0 求得
=(
,0,1),计算cos<
>的值,可得MN与平面PAB所成角的正弦值.
| PM |
| PA |
| BM |
| BD |
| 1 |
| 3 |
| PM |
| PA |
| BN |
| BD |
| 1 |
| 3 |
(Ⅰ)设AC与BD的交点为O,AB=PA=2.如图所示,建立空间直角坐标系,求得A、B、C、D的坐标.求得
| OM |
| OA |
| AM |
| OA |
| 2 |
| 3 |
| AP |
| ON |
| 1 |
| 3 |
| OB |
坐标,可得
| AN |
| AD |
| MN |
| AD |
(Ⅱ)设平面PBC的法向量为
| n |
| n |
| BP |
| n |
| BC |
| n |
| n |
| MN |
(Ⅲ)设平面PAB的法向量为
| n |
| AP |
| n |
| n |
| AB |
| n |
| 2 |
| MN |
| n |
解答: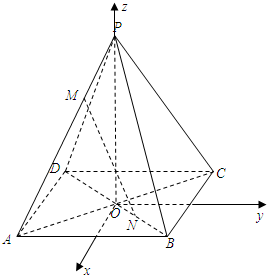 (Ⅰ)设AC与BD的交点为O,AB=PA=2.以点O为坐标原点,
(Ⅰ)设AC与BD的交点为O,AB=PA=2.以点O为坐标原点,
,
方向分别是x轴、y轴正方向,
建立空间直角坐标系O-xyz.
则A(1,-1,0),B(1,1,0),C(-1,1,0),D(-1,-1,0),…(2分)
设P(0,0,p),则
=(-1,1,p),又AP=2,∴1+1+p2=4,∴p=
,
∵
=
+
=
+
=(
,-
,
),
=
=(
,
,0),
∴
=(0,
,-
),
=(-2,0,0),
∵
•
=0,∴异面直线MN与AD所成角为90°.…(8分)
(Ⅱ)∵
=(-1,-1,
),
设平面PBC的法向量为
=(a,b,c),∵
•
=0,
•
=0,则
,…(10分)
取
=(0
1)=,∵
•
,∴MN∥平面PBC. …(14分)
(Ⅲ)设平面PAB的法向量为
=(x,y,z),
=(-1,1,
)
=(0,2,0)
由
⊥
⊥
,
∴
•
=0
•
=0 则
,…(16分)
取
=(
,0,1),cos<
>=
=-
,
∴MN与平面PAB所成角的正弦值是
.…(20分)
 (Ⅰ)设AC与BD的交点为O,AB=PA=2.以点O为坐标原点,
(Ⅰ)设AC与BD的交点为O,AB=PA=2.以点O为坐标原点,| DA |
| AB |
建立空间直角坐标系O-xyz.
则A(1,-1,0),B(1,1,0),C(-1,1,0),D(-1,-1,0),…(2分)
设P(0,0,p),则
| AP |
| 2 |
∵
| OM |
| OA |
| AM |
| OA |
| 2 |
| 3 |
| AP |
| 1 |
| 3 |
| 1 |
| 3 |
2
| ||
| 3 |
| ON |
| 1 |
| 3 |
| OB |
| 1 |
| 3 |
| 1 |
| 3 |
∴
| AN |
| 2 |
| 3 |
2
| ||
| 3 |
| AD |
∵
| MN |
| AD |
(Ⅱ)∵
| BP |
| 2 |
设平面PBC的法向量为
| n |
| n |
| BP |
| n |
| BC |
|
取
| n |
| 2 |
| n |
| MN |
(Ⅲ)设平面PAB的法向量为
| n |
| AP |
| 2 |
| AB |
由
| AP |
| n |
| AB |
| n |
∴
| AP |
| n |
| n |
| AB |
|
取
| n |
| 2 |
| MN |
| n |
-
| ||||||
|
| ||
| 3 |
∴MN与平面PAB所成角的正弦值是
| 2 |
| 3 |
点评:本题主要考查异面直线所成的角的定义和求法,直线和平面垂直的判定定理的应用,直线和平面所成的角的定义和求法,两个向量垂直的性质和条件,
两个向量坐标形式的运算,属于中档题.
两个向量坐标形式的运算,属于中档题.

练习册系列答案
相关题目
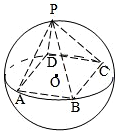 如图,正四棱锥P-ABCD底面的四个顶点A、B、C、D在球O的同一个大圆上,点P在球面上,若
如图,正四棱锥P-ABCD底面的四个顶点A、B、C、D在球O的同一个大圆上,点P在球面上,若 如图,正四棱锥P-ABCD的所有棱长相等,E为PC的中点,则异面直线BE与PA所成角的余弦值是( )
如图,正四棱锥P-ABCD的所有棱长相等,E为PC的中点,则异面直线BE与PA所成角的余弦值是( ) (2008•上海一模)如图,正四棱锥P-ABCD底面的四个顶点A,B,C,D在球O的同一个大圆上,点P在球面上,且已知
(2008•上海一模)如图,正四棱锥P-ABCD底面的四个顶点A,B,C,D在球O的同一个大圆上,点P在球面上,且已知 如图,正四棱锥P-ABCD中,PA=2,AB=1,M是侧棱PC的中点,O为底面正方形的中心.
如图,正四棱锥P-ABCD中,PA=2,AB=1,M是侧棱PC的中点,O为底面正方形的中心. (2009•温州一模)如图是正四棱锥P-ABCD的三视图,其中正视图是边长为1的正三角形,则这个四棱锥的表面积是( )
(2009•温州一模)如图是正四棱锥P-ABCD的三视图,其中正视图是边长为1的正三角形,则这个四棱锥的表面积是( )