��Ŀ����
2����֪��Բ$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1��a��b��0����������Ϊ$\frac{{\sqrt{6}}}{3}$��������Բ���ĸ�����õ����ı��ε����Ϊ4$\sqrt{3}$����1������Բ�ķ��̣�
��2�����㣨m��0����m��$\sqrt{6}$����б��Ϊ-$\frac{{\sqrt{3}}}{3}$��ֱ��l����Բ��C��D���㣬FΪ��Բ���ҽ��㣬���|CD|2=4|FC|•|FD|�����CFD�Ĵ�С��
���� ��1���������ʿɵ�a��b�Ĺ�ϵ������������Բ���ĸ�����õ����ı��ε����Ϊ$4\sqrt{3}$���õ�a��b����һ��ϵ���������a��b�ô𰸣�
��2���������ֱ��l�ķ���Ϊ$y=-\frac{\sqrt{3}}{3}��x-m����m��\sqrt{6}��$������ֱ�߷�������Բ���̣��ɡ���0���m�ķ�Χ�������ø���ϵ���Ĺ�ϵ���C��D���������ĺ��������һ����|CD||FC|�ú���m�Ĵ���ʽ��ʾ�����|CD|2=4|FC|•|FD|���m=3���ɵ�$\overrightarrow{FC}•\overrightarrow{FD}=��{x}_{1}-2����{x}_{2}-2��+{y}_{1}{y}_{2}$=$\frac{4}{3}{x}_{1}{x}_{2}-\frac{m+6}{3}��{x}_{1}{+x}_{2}��+\frac{{m}^{2}}{3}+4$=$\frac{2��{m}^{2}-3m��}{3}=0$��
���CFD�Ĵ�С����
��� 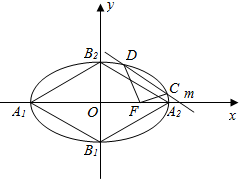 �⣺��ͼ��
�⣺��ͼ��
��1����$e=\frac{c}{a}=\sqrt{1-\frac{b^2}{a^2}}=\frac{{\sqrt{6}}}{3}$����$a=\sqrt{3}b$��
��������Բ���ĸ�����õ����ı��ε����Ϊ$4\sqrt{3}$��
��$2ab=4\sqrt{3}$����$ab=2\sqrt{3}$��
��a2=6��b2=2�������Բ�ķ���Ϊ$\frac{x^2}{6}+\frac{y^2}{2}=1$��
��2���������ֱ��l�ķ���Ϊ$y=-\frac{\sqrt{3}}{3}��x-m����m��\sqrt{6}��$��
��$\left\{\begin{array}{l}{\frac{{x}^{2}}{6}+\frac{{y}^{2}}{2}=1}\\{y=-\frac{\sqrt{3}}{3}��x-m��}\end{array}\right.$����2x2-2mx+m2-6=0��
�ɡ�=4m2-8��m2-6����0�����$-2\sqrt{3}��m��2\sqrt{3}$��
��m$��\sqrt{6}$����$\sqrt{6}��m��2\sqrt{3}$��
��C��x1��y1����D��x2��y2����
��${x}_{1}+{x}_{2}=m��{x}_{1}{x}_{2}=\frac{{m}^{2}-6}{2}$��
��|CD|=$\sqrt{1+��-\frac{\sqrt{3}}{3}��^{2}}•\sqrt{��{x}_{1}+{x}_{2}��^{2}-4{x}_{1}{x}_{2}}$=$\frac{2}{3}\sqrt{3}•\sqrt{12-{m}^{2}}$��
�֡�|FC|=$\sqrt{��{x}_{1}-2��^{2}+{{y}_{1}}^{2}}=\sqrt{��{{x}_{1}}^{2}-4{x}_{1}+4��+\frac{6-{{x}_{1}}^{2}}{3}}$=$\sqrt{\frac{2}{3}}��3-{x}_{1}��$��
|FD|=$\sqrt{��{x}_{2}-2��^{2}+{{y}_{2}}^{2}}=\sqrt{��{{x}_{2}}^{2}-4{x}_{2}+4��+\frac{6-{{x}_{2}}^{2}}{3}}$=$\sqrt{\frac{2}{3}}��3-{x}_{2}��$��
|FC||FD|=$\frac{2}{3}��3-{x}_{1}����3-{x}_{2}��=\frac{2}{3}[{x}_{1}{x}_{2}-3��{x}_{1}+{x}_{2}��+9]$=$\frac{1}{3}��{m}^{2}-6m+12��$��
��|CD|2=4|FC|•|FD|����$\frac{4}{3}��12-m��^{2}=\frac{4}{3}��{m}^{2}-6m+12��$�����m=0��m=3��
��$\sqrt{6}��m��2\sqrt{3}$����m=3��
�֡�$\overrightarrow{FC}=��{x}_{1}-2��{y}_{1}����\overrightarrow{FD}=��{x}_{2}-2��{y}_{2}��$��
��${y}_{1}{y}_{2}=[-\frac{\sqrt{3}}{3}��{x}_{1}-m��]•[-\frac{\sqrt{3}}{3}��{x}_{2}-m��]$=$\frac{1}{3}{x}_{1}{x}_{2}-\frac{m}{3}��{x}_{1}+{x}_{2}��+\frac{{m}^{2}}{3}$��
��$\overrightarrow{FC}•\overrightarrow{FD}=��{x}_{1}-2����{x}_{2}-2��+{y}_{1}{y}_{2}$=$\frac{4}{3}{x}_{1}{x}_{2}-\frac{m+6}{3}��{x}_{1}{+x}_{2}��+\frac{{m}^{2}}{3}+4$=$\frac{2��{m}^{2}-3m��}{3}=0$��
���CFD=90�㣮
���� ���⿼����Բ���̵�����������Բ�ļ����ʣ�����ֱ����Բ����λ�ù�ϵ��Ӧ�ã��漰ֱ����Բ���ߵĹ�ϵ���⣬�����ð�ֱ�߷��̺�Բ���߷������������ø���ϵ���Ĺ�ϵ��⣬ѵ����ƽ�����������Բ���������е�Ӧ�ã���ѹ���⣮

 ϰ�⾫ѡϵ�д�
ϰ�⾫ѡϵ�д�| A�� | ���ֵΪ$\frac{8}{{e}^{2}}$ | B�� | ���ֵΪ$\frac{4}{{e}^{2}}$ | C�� | ��СֵΪ$\frac{8}{{e}^{2}}$ | D�� | ��СֵΪ$\frac{4}{{e}^{2}}$ |
| A�� | ��1��2�� | B�� | ��$\frac{3}{4}$��1�� | C�� | ��$\frac{2}{3}$��$\frac{3}{4}$�� | D�� | ��0��$\frac{2}{3}$�� |
| A�� | ��$\frac{4}{5}$��1�� | B�� | ��$\frac{4}{5}$��+�ޣ� | C�� | ��0��$\frac{4}{5}$���ȣ�1��+�ޣ� | D�� | ��0��$\frac{4}{5}$���ȣ�$\frac{4}{5}$��+�ޣ� |