题目内容
16.若曲线C1,y=x2与曲线C2:y=aex存在公切线,则a的( )| A. | 最大值为$\frac{8}{{e}^{2}}$ | B. | 最大值为$\frac{4}{{e}^{2}}$ | C. | 最小值为$\frac{8}{{e}^{2}}$ | D. | 最小值为$\frac{4}{{e}^{2}}$ |
分析 分别求出两个函数的导函数,由两函数在切点处的导数相等,并由斜率公式,得到由此得到m=2n-2,则4n-4=aen有解.再由导数即可进一步求得a的最值.
解答 解:y=x2在点(m,m2)的切线斜率为2m,
y=aex在点(n,aen)的切线斜率为aen,
如果两个曲线存在公共切线,那么:2m=aen.
又由斜率公式得到,2m=$\frac{{m}^{2}-a{e}^{n}}{m-n}$,
由此得到m=2n-2,
则4n-4=aen有解.
由y=4x-4,y=aex的图象有交点即可.
设切点为(s,t),则aes=4,且t=4s-4=aes,
即有切点(2,4),a=$\frac{4}{{e}^{2}}$,
故a的取值范围是:0<a≤$\frac{4}{{e}^{2}}$,
即a的最大值为$\frac{4}{{e}^{2}}$.
故选:B.
点评 本题考查利用导数研究曲线上某点的切线方程,过曲线上某点处的切线的斜率,就是函数在该点处的导数值,是中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
6.对任意$x∈({0,\frac{π}{2}})$,不等式sinx•f(x)<cosx•f′(x)恒成立,则下列不等式错误的是( )
| A. | $f({\frac{π}{3}})>\sqrt{2}f({\frac{π}{4}})$ | B. | $f({\frac{π}{3}})>2cos1•f(1)$ | C. | $f({\frac{π}{4}})<\sqrt{2}cos1•f(1)$ | D. | $f({\frac{π}{4}})<\frac{{\sqrt{6}}}{2}f({\frac{π}{6}})$ |
11.下列命题是假命题的是( )
| A. | 若$\overrightarrow{a}•\overrightarrow{b}$=0($\overrightarrow{a}$≠0,$\overrightarrow{b}$≠0),则$\overrightarrow{a}⊥\overrightarrow{b}$ | B. | 若|$\overrightarrow{a}$|=|$\overrightarrow{b}$|,则$\overrightarrow{a}$=$\overrightarrow{b}$ | ||
| C. | 若ac2>bc2,则a>b | D. | 若α=60°,则cosα=$\frac{1}{2}$ |
6.设奇函数f(x)在(-∞,0)上为减函数,且f(2)=0,则$\frac{{f(x)-3f({-x})}}{2x}>0$的解集为( )
| A. | (-2,0)∪(2,+∞) | B. | (-∞,-2)∪(0,2) | C. | (-∞.-2)∪(2.+∞) | D. | (-2,0)∪(0,2) |
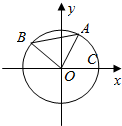 已知A,B是单位圆O上的动点,且A,B分别在第一,二象限.C是圆与x轴正半轴的交点,△AOB为正三角形,记∠AOC=α
已知A,B是单位圆O上的动点,且A,B分别在第一,二象限.C是圆与x轴正半轴的交点,△AOB为正三角形,记∠AOC=α