题目内容
设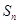 表示数列
表示数列 的前
的前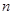 项和.
项和.
(1)若 为公比为
为公比为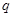 的等比数列,写出并推导
的等比数列,写出并推导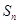 的计算公式;
的计算公式;
(2)若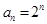 ,
,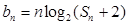 ,求证:
,求证: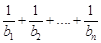 <1.
<1.
(1)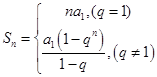 ;(2)证明过程详见试题解析.
;(2)证明过程详见试题解析.
解析试题分析:(1)利用错位相减法进行推导,先写出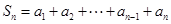 ,然后将此式两边同时乘以公比
,然后将此式两边同时乘以公比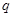 ,得到
,得到 ,两式相减可得:
,两式相减可得: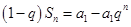 ,所以当
,所以当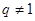 时,有
时,有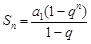 ,但是要注意当
,但是要注意当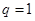 时,
时,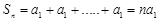 ;(2)若
;(2)若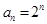 ,
,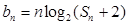 ,那么
,那么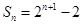 ,所以
,所以 .注意到
.注意到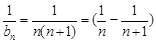 ,证明过程中采用裂项相消法进行,有
,证明过程中采用裂项相消法进行,有 .
.
试题解析:(1)因为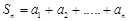
所以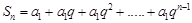 ①
①
将①式乘以公比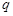 ,可得
,可得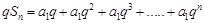 ②
②
①-②得: 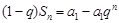
所以当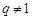 时,
时,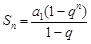
当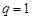 时,
时,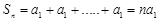
因此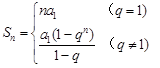
(2)证明:因为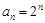 ,所以
,所以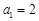 ,
,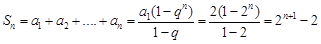
所以
因此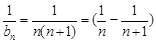
则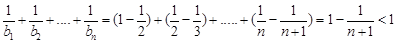
考点:等比数列前 项和;数列不等式证明.
项和;数列不等式证明.

练习册系列答案
相关题目
 的通项公式为
的通项公式为 ,等比数列
,等比数列 满足
满足 .
. 项和
项和 ;
; ,求数列
,求数列 的前
的前 项和
项和 .
. 个正数
个正数 使得这
使得这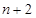 个数构成递增的等比数列,将这
个数构成递增的等比数列,将这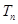 ,令
,令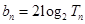 .
.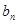 }的通项公式;
}的通项公式;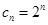 ,设
,设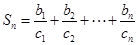 ,求
,求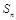 .
.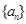 的公比为q,且
的公比为q,且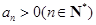 ,
,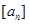 表示不超过实数
表示不超过实数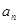 的最大整数(如
的最大整数(如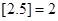 ),记
),记 ,数列
,数列 项和为
项和为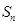 ,数列
,数列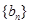 的前
的前 .
.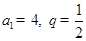 ,求
,求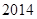 的正整数n,都有
的正整数n,都有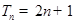 ,证明:
,证明: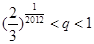 .
.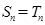 (
(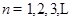 )的充分必要条件为
)的充分必要条件为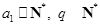 .
.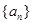 为等比数列,其前
为等比数列,其前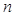 项和为
项和为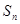 ,已知
,已知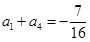 ,且
,且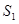 ,
,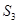 ,
,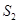 成等差,
成等差,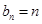 (
(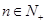 ),记
),记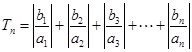 ,若
,若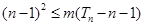 对于
对于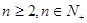 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.