题目内容
已知函数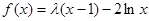 ,
,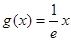 ,(
,(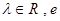 为自然对数的底数).
为自然对数的底数).
(Ⅰ)当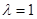 时,求函数
时,求函数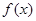 的单调区间;
的单调区间;
(Ⅱ)函数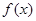 在区间
在区间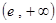 上恒为正数,求
上恒为正数,求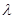 的最小值;
的最小值;
(Ⅲ)若对任意给定的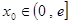 ,在
,在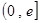 上总存在两个不同的
上总存在两个不同的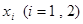 ,使得
,使得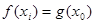 成立,求
成立,求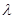 的取值范围.
的取值范围.
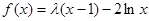 ,
,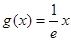 ,(
,(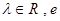 为自然对数的底数).
为自然对数的底数).(Ⅰ)当
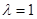 时,求函数
时,求函数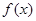 的单调区间;
的单调区间;(Ⅱ)函数
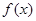 在区间
在区间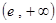 上恒为正数,求
上恒为正数,求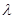 的最小值;
的最小值;(Ⅲ)若对任意给定的
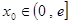 ,在
,在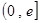 上总存在两个不同的
上总存在两个不同的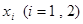 ,使得
,使得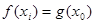 成立,求
成立,求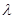 的取值范围.
的取值范围.(Ⅰ)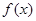 的单调减区间为
的单调减区间为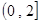 ,单调增区间为
,单调增区间为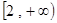 (Ⅱ)
(Ⅱ)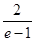 (Ⅲ)
(Ⅲ)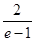
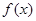 的单调减区间为
的单调减区间为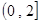 ,单调增区间为
,单调增区间为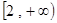 (Ⅱ)
(Ⅱ)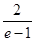 (Ⅲ)
(Ⅲ)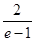
试题分析:(Ⅰ)函数f (x)的定义域为
 ,
,当
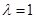 时,
时,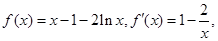
由
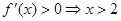 , 由
, 由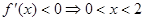 .
.故
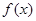 的单调减区间为
的单调减区间为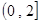 ,单调增区间为
,单调增区间为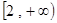 . ……4分
. ……4分(Ⅱ)
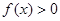 在
在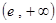 恒成立等价于:
恒成立等价于: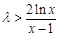 在
在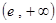 恒成立,
恒成立,令
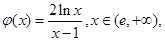 则
则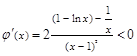 ,x∈
,x∈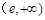 ,
,于是
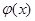 在
在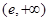 上为减函数,又在x=e处连续,
上为减函数,又在x=e处连续,故在
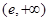 ,
,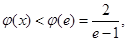
从而要使
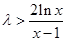 对任意的
对任意的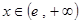 恒成立.
恒成立.只要
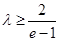 ,故
,故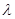 的最小值为
的最小值为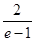 . ……9分
. ……9分(Ⅲ)一次函数
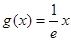 在
在 上递增,故函数
上递增,故函数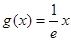 在
在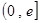 上的值域是
上的值域是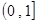 .
.当
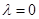 时,
时,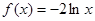 为单调递减函数,不合题意;
为单调递减函数,不合题意;当
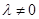 时,
时,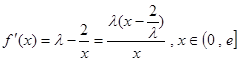 ,
,要使
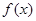 在
在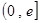 不单调,只要
不单调,只要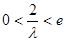 ,此时
,此时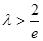 ①
①故
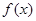 在
在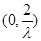 上单调递减,在
上单调递减,在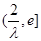 上单调递增.
上单调递增.注意到
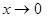 时,
时,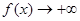
∴
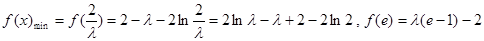
∴对任意给定的
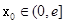 ,在区间
,在区间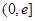 上总存在两个不同的
上总存在两个不同的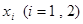 使得
使得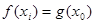 成立,当且仅当
成立,当且仅当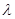 满足下列条件
满足下列条件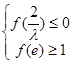 ,即
,即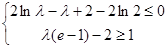
令
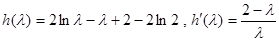 ,
,当
 时,
时,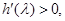 函数
函数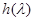 单调递增;
单调递增;当
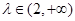 时,
时,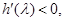 函数
函数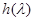 单调递减.
单调递减.所以,当
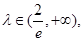 时有
时有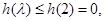 即
即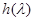 对任意
对任意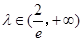 恒成立.
恒成立.又由
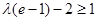 ,解得
,解得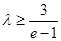 ……②
……②∴ 综合①②可知,当
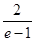 时,对任意给定的
时,对任意给定的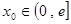 ,在
,在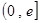 上总存在两个不同的
上总存在两个不同的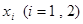 ,使
,使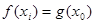 成立. ……14分
成立. ……14分点评:导数是研究函数性质的有力工具,研究单调性、极值、最值时不要忘记先求函数的定义域,而不等式恒成立问题,一般转化为函数的最值问题解决,分类讨论时要注意分类标准要不重不漏.

练习册系列答案
相关题目
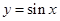 的图象向左平移
的图象向左平移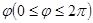 个单位后,得到函数
个单位后,得到函数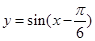 的图象,则
的图象,则 等于( )
等于( )
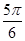

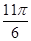
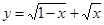 的定义域为( )
的定义域为( )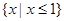
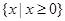
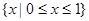
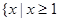 或
或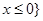
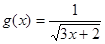 的定义域为 。
的定义域为 。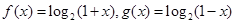 ,则f(x)-g(x)是
,则f(x)-g(x)是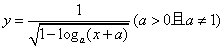 的定义域.
的定义域.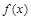 ,当
,当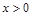 时,
时,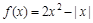 ,则
,则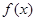 在
在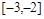 上是( )
上是( )
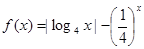 的零点分别为
的零点分别为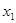 ,
,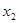 ,则( )
,则( )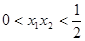

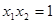
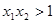
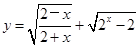 的定义域为
的定义域为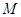 ,
,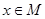 时,求函数
时,求函数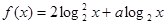 的最大值。
的最大值。