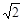题目内容
对于三次函数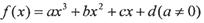 ,定义
,定义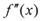 是
是 的导函数
的导函数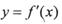 的导函数,若方程
的导函数,若方程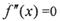 有实数解x0,则称点
有实数解x0,则称点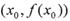 为函数
为函数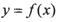 的“拐点”,可以发现,任何三次函数都有“拐点”,任何三次函数都有对称中心,且“拐点”就是对称中心,请你根据这一发现判断下列命题:
的“拐点”,可以发现,任何三次函数都有“拐点”,任何三次函数都有对称中心,且“拐点”就是对称中心,请你根据这一发现判断下列命题:
①任意三次函数都关于点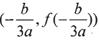 对称:
对称:
②存在三次函数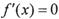 有实数解
有实数解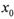 ,点
,点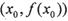 为
为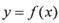 的对称中心;
的对称中心;
③存在三次函数有两个及两个以上的对称中心;
④若函数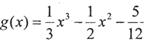 ,则,
,则,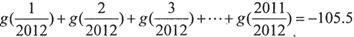 .
.
其中正确命题的序号为_______(把所有正确命题的序号都填上).
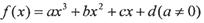 ,定义
,定义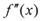 是
是 的导函数
的导函数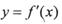 的导函数,若方程
的导函数,若方程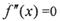 有实数解x0,则称点
有实数解x0,则称点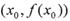 为函数
为函数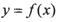 的“拐点”,可以发现,任何三次函数都有“拐点”,任何三次函数都有对称中心,且“拐点”就是对称中心,请你根据这一发现判断下列命题:
的“拐点”,可以发现,任何三次函数都有“拐点”,任何三次函数都有对称中心,且“拐点”就是对称中心,请你根据这一发现判断下列命题:①任意三次函数都关于点
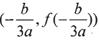 对称:
对称:②存在三次函数
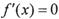 有实数解
有实数解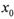 ,点
,点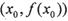 为
为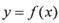 的对称中心;
的对称中心;③存在三次函数有两个及两个以上的对称中心;
④若函数
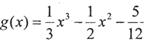 ,则,
,则,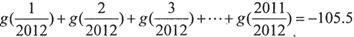 .
.其中正确命题的序号为_______(把所有正确命题的序号都填上).
①②
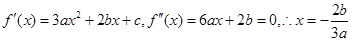 ,所以其对称中心为
,所以其对称中心为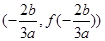 ,①正确.对于②,若
,①正确.对于②,若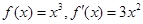 ,x=0是
,x=0是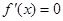 的解,(0,f(0)就是函数y=f(x)的对称中心.故②正确.由于三次函数两次求导之后,只有一个根.所以对称中心也只有一个.故③错.对于④,
的解,(0,f(0)就是函数y=f(x)的对称中心.故②正确.由于三次函数两次求导之后,只有一个根.所以对称中心也只有一个.故③错.对于④,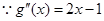 ,所以其对称中心为
,所以其对称中心为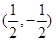 ,
,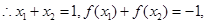 由于
由于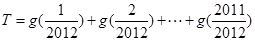 ,
,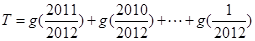 ,
,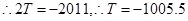 ,故④错.
,故④错.
练习册系列答案
相关题目
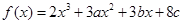 在
在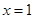 及
及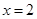 时取得极值.(Ⅰ)求a、b的值;(Ⅱ)若对于任意的
时取得极值.(Ⅰ)求a、b的值;(Ⅱ)若对于任意的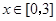 ,都有
,都有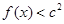 成立,求c的取值范围.
成立,求c的取值范围.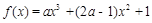 ,当
,当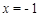 时,函数
时,函数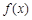 取得极值.
取得极值. 的值;
的值;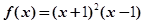 ,
,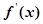 ;
; 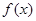 的单调区间;
的单调区间; 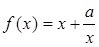 且
且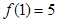 .
. 的值;
的值; 在
在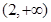 上的单调性,并证明你的结论.
上的单调性,并证明你的结论.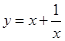 在区间
在区间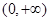 的单调递增区间是________________,单调递减区间是__________
的单调递增区间是________________,单调递减区间是__________ 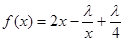 在(1,+∞)上是增函数,则实数
在(1,+∞)上是增函数,则实数  的取值范围是( )
的取值范围是( )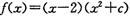 在
在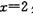 处有极值,则函数
处有极值,则函数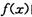 的图象在
的图象在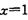 处的切线的斜率为( )
处的切线的斜率为( )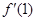 =2,则a的值为
=2,则a的值为