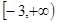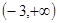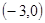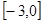题目内容
(本题满分15分)
设函数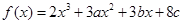 在
在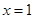 及
及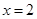 时取得极值.(Ⅰ)求a、b的值;(Ⅱ)若对于任意的
时取得极值.(Ⅰ)求a、b的值;(Ⅱ)若对于任意的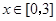 ,都有
,都有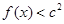 成立,求c的取值范围.
成立,求c的取值范围.
设函数
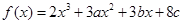 在
在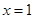 及
及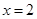 时取得极值.(Ⅰ)求a、b的值;(Ⅱ)若对于任意的
时取得极值.(Ⅰ)求a、b的值;(Ⅱ)若对于任意的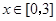 ,都有
,都有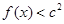 成立,求c的取值范围.
成立,求c的取值范围.(Ⅰ) ,
,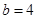
(Ⅱ)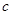 的取值范围为
的取值范围为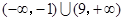
 ,
,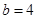
(Ⅱ)
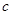 的取值范围为
的取值范围为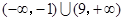
解:(Ⅰ)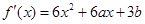 ,
,
因为函数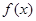 在
在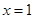 及
及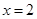 取得极值,则有
取得极值,则有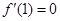 ,
,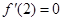 .
.
即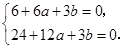 ……5分
……5分
解得 ,
,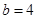 .……7分
.……7分
(Ⅱ)由(Ⅰ)可知,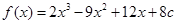 ,
,
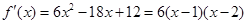 .
.
当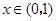 时,
时,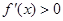 ;
;
当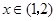 时,
时,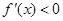 ;
;
当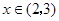 时,
时,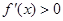 .……10分
.……10分
所以,当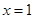 时,
时,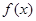 取得极大值
取得极大值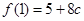 ,又
,又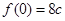 ,
,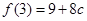 .
.
则当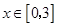 时,
时,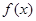 的最大值为
的最大值为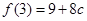 .……12分
.……12分
因为对于任意的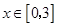 ,有
,有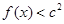 恒成立,
恒成立,
所以 ,
,
解得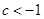 或
或 ,
,
因此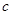 的取值范围为
的取值范围为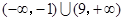 ……15分
……15分
思路分析:第一问中,利用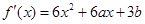 ,因为函数
,因为函数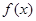 在
在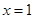 及
及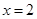 取得极值,则有
取得极值,则有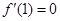 ,
,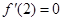 得到解析式
得到解析式
第二问中,对于任意的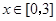 ,都有
,都有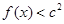 成立只需要求解y=f(x)的最大值即可。
成立只需要求解y=f(x)的最大值即可。
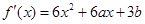 ,
,因为函数
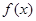 在
在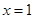 及
及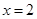 取得极值,则有
取得极值,则有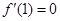 ,
,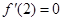 .
.即
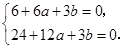 ……5分
……5分解得
 ,
,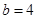 .……7分
.……7分(Ⅱ)由(Ⅰ)可知,
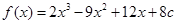 ,
,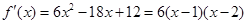 .
.当
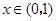 时,
时,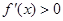 ;
;当
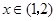 时,
时,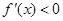 ;
;当
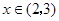 时,
时,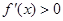 .……10分
.……10分所以,当
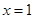 时,
时,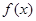 取得极大值
取得极大值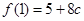 ,又
,又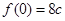 ,
,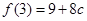 .
.则当
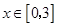 时,
时,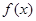 的最大值为
的最大值为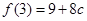 .……12分
.……12分因为对于任意的
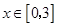 ,有
,有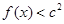 恒成立,
恒成立,所以
 ,
,解得
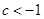 或
或 ,
,因此
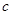 的取值范围为
的取值范围为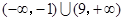 ……15分
……15分思路分析:第一问中,利用
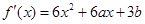 ,因为函数
,因为函数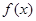 在
在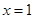 及
及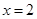 取得极值,则有
取得极值,则有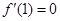 ,
,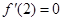 得到解析式
得到解析式第二问中,对于任意的
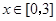 ,都有
,都有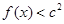 成立只需要求解y=f(x)的最大值即可。
成立只需要求解y=f(x)的最大值即可。
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
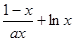 在[1,+∞
在[1,+∞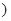 上为增函数.
上为增函数. 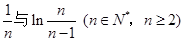 的大小,说明理由;
的大小,说明理由; (n∈N*, n≥2)
(n∈N*, n≥2)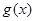 是定义在
是定义在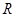 上、以2为周期的函数,若
上、以2为周期的函数,若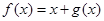 在
在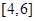 上的值域为
上的值域为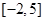 ,则
,则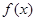 在区间
在区间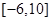 上的值域为 .
上的值域为 .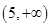 上为增函数,且满足
上为增函数,且满足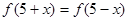 ,则( )
,则( )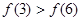
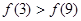
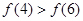
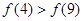
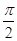 ―2x);②f(x)=sinx+cosx;③ f(x)=sinxcosx;
―2x);②f(x)=sinx+cosx;③ f(x)=sinxcosx;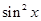 ;⑤ f(x)=|cos2x|
;⑤ f(x)=|cos2x|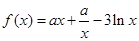
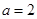 时,求函数
时,求函数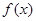 的单调区间;
的单调区间;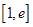 上是单调函数,求
上是单调函数,求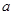 的取值范围.
的取值范围.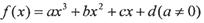 ,定义
,定义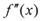 是
是 的导函数
的导函数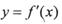 的导函数,若方程
的导函数,若方程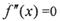 有实数解x0,则称点
有实数解x0,则称点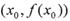 为函数
为函数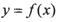 的“拐点”,可以发现,任何三次函数都有“拐点”,任何三次函数都有对称中心,且“拐点”就是对称中心,请你根据这一发现判断下列命题:
的“拐点”,可以发现,任何三次函数都有“拐点”,任何三次函数都有对称中心,且“拐点”就是对称中心,请你根据这一发现判断下列命题: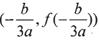 对称:
对称: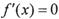 有实数解
有实数解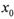 ,点
,点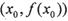 为
为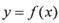 的对称中心;
的对称中心;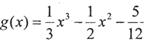 ,则,
,则,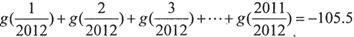 .
.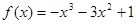 在
在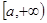 上的最大值为1,则
上的最大值为1,则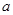 的取值范围是( )
的取值范围是( )