题目内容
如图,直三棱柱 中,AB=1,BC=2,
中,AB=1,BC=2, ,M为线段
,M为线段 上的一动点,当
上的一动点,当 最小时,点C到平面
最小时,点C到平面 的距离为( )
的距离为( )
| A.6 | B.3 | C. | D. |
D
解析试题分析:将直三棱柱 沿棱
沿棱 展开成平面,连接
展开成平面,连接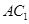 与
与 的交点即为满足
的交点即为满足 最小时的点M. 由于AB=1,BC=2,
最小时的点M. 由于AB=1,BC=2,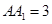 ,再结合棱柱的性质,可得
,再结合棱柱的性质,可得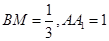 ,故
,故 . 由展开的平面图形得
. 由展开的平面图形得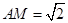 ,
,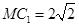 ,由直三棱柱可得
,由直三棱柱可得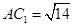 ,所以
,所以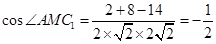 ,故
,故 ,
,
所以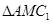 的面积为
的面积为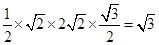 . 由
. 由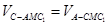 ,得
,得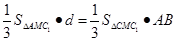 ,所以
,所以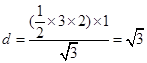 .
.
考点:点到平面的距离、等体积转化.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
教室内有一把直尺,无论怎样放置,地面上总有这样的直线与该直尺所在直线 ( ).
| A.平行 | B.异面 | C.垂直 | D.相交但不垂直 |
已知不同直线 、
、 和不同平面
和不同平面 、
、 ,给出下列命题:
,给出下列命题:
① ②
② ③
③ 异面
异面
④ 其中错误的命题有( )个
其中错误的命题有( )个
| A.1 | B.2 | C.3 | D.4 |
设a,b为两条不同的直线,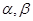 为两个不同的平面,则下列说法正确的是( )
为两个不同的平面,则下列说法正确的是( )
| A.若a∥α,α⊥β,则a∥β | B.若a∥b,a⊥β,则b⊥β |
| C.若a∥α,b∥α,则a∥b | D.若a⊥b,a∥α,则b⊥α |
设 是两条不同的直线,
是两条不同的直线, 是三个不同的平面,则下列命题正确的是( )
是三个不同的平面,则下列命题正确的是( )
A.若 , , ,则 ,则 | B.若 与 与 所成的角相等,则 所成的角相等,则 |
C.若 , , ,则 ,则 | D.若 , ,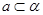 ,则 ,则 |
已知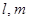 是两条不同的直线,
是两条不同的直线,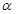 是一个平面,且
是一个平面,且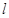 ∥
∥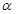 ,则下列命题正确的是( )
,则下列命题正确的是( )
A.若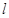 ∥ ∥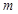 ,则 ,则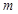 ∥ ∥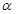 | B.若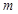 ∥ ∥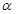 ,则 ,则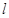 ∥ ∥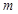 |
C.若 ,则 ,则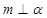 | D.若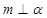 ,则 ,则 |
设m,n是两条不同的直线,α,β是两个不同的平面,下列命题中正确的是( )
| A.若α⊥β,m?α,n?β,则m⊥n |
| B.若α∥β,m?α,n?β,则m∥n |
| C.若m⊥n,m?α,n?β,则α⊥β |
| D.若m⊥α,m∥n,n∥β,则α⊥β |
已知m,n为异面直线,m⊥平面α,n⊥平面β.直线l满足l⊥m,l⊥n,l?α,l?β,则( )
| A.α∥β且l∥α |
| B.α⊥β且l⊥β |
| C.α与β相交,且交线垂直于l |
| D.α与β相交,且交线平行于l |
设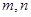 是两条不同的直线,
是两条不同的直线, 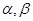 是两个不同的平面,则下列命题正确的是( )
是两个不同的平面,则下列命题正确的是( )
A.若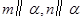 ,则 ,则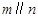 | B.若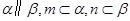 ,则 ,则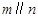 |
C.若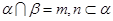 ,则 ,则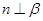 | D.若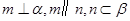 ,则 ,则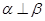 |