题目内容
设a,b为两条不同的直线,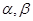 为两个不同的平面,则下列说法正确的是( )
为两个不同的平面,则下列说法正确的是( )
| A.若a∥α,α⊥β,则a∥β | B.若a∥b,a⊥β,则b⊥β |
| C.若a∥α,b∥α,则a∥b | D.若a⊥b,a∥α,则b⊥α |
B
解析试题分析:对A. 若a与β相交、垂直或a∥β都 有可能. B显然成立.对C.a、b平行、相交或异面都有可能.对D. b∥α或b⊥α都有可能.
考点:空间直线、平面间的位置关系.

练习册系列答案
相关题目
设 ,b,c是空间三条不同的直线,
,b,c是空间三条不同的直线, ,
, 是空间两个不同的平面,则下列命题不成立的是( )
是空间两个不同的平面,则下列命题不成立的是( )
A.当 时,若 时,若 ⊥ ⊥ ,则 ,则 ∥ ∥ |
B.当 ,且 ,且 是 是 在 在 内的射影时,若b⊥c,则 内的射影时,若b⊥c,则 ⊥b ⊥b |
C.当 时,若b⊥ 时,若b⊥ ,则 ,则 |
D.当 时,若c∥ 时,若c∥ ,则b∥c ,则b∥c |
下列命题正确的是( )
| A.若两条直线和同一个平面所成的角相等,则这两条直线平行 |
| B.若一个平面内有三个点到另一个平面的距离相等,则这两个平面平行 |
| C.若一条直线平行于两个相交平面,则这条直线与这两个平面的交线平行 |
| D.若两个平面都垂直于第三个平面,则这两个平面平行 |
若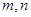 是两条不同的直线,
是两条不同的直线,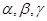 是三个不同的平面,则下列命题中正确命题是( )
是三个不同的平面,则下列命题中正确命题是( )
A.若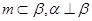 ,则 ,则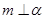 |
B.若 , ,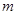 ∥ ∥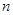 ,则 ,则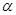 ∥ ∥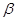 |
C.若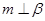 , ,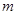 ∥ ∥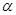 ,则 ,则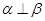 |
D.若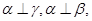 则 则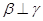 |
如图所示,在四边形ABCD中,AD∥BC,AD=AB,∠BCD=45°,∠BAD=90°,将△ABD沿BD折起,使平面ABD⊥平面BCD,构成三棱锥A—BCD,则在三棱锥A—BCD中,下列命题正确的是( )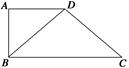
| A.平面ABD⊥平面ABC |
| B.平面ADC⊥平面BDC |
| C.平面ABC⊥平面BDC |
| D.平面ADC⊥平面ABC |
如图所示,正方体 的棱长为a,M、N分别为
的棱长为a,M、N分别为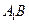 和AC上的点,
和AC上的点, ,则MN与平面
,则MN与平面 的位置关系是( )
的位置关系是( )
| A.相交 | B.平行 | C.垂直 | D.不能确定 |
在空间,下列命题正确的是( )
| A.平行直线的平行投影重合 |
| B.平行于同一直线的两个平面平行 |
| C.垂直于同一平面的两个平面平行 |
| D.垂直于同一平面的两条直线平行 |
 中,AB=1,BC=2,
中,AB=1,BC=2, ,M为线段
,M为线段 上的一动点,当
上的一动点,当 最小时,点C到平面
最小时,点C到平面 的距离为( )
的距离为( )


 是两条不重合的直线,
是两条不重合的直线, 是两个不重合的平面,给出下列命题:
是两个不重合的平面,给出下列命题: ,
, ,且
,且 ,则
,则 ;
; ,且
,且 ,
, ,则
,则 ;
;