题目内容
如图,已知抛物线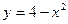 与直线
与直线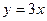 的两个交点分别为A、B,点P在抛物线上从A向B运动(点P不同于点A、B),
的两个交点分别为A、B,点P在抛物线上从A向B运动(点P不同于点A、B),

(Ⅰ)求由抛物线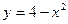 与直线
与直线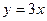 所围成的图形面积;
所围成的图形面积;
(Ⅱ)求使⊿PAB的面积为最大时P点的坐标。
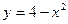 与直线
与直线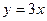 的两个交点分别为A、B,点P在抛物线上从A向B运动(点P不同于点A、B),
的两个交点分别为A、B,点P在抛物线上从A向B运动(点P不同于点A、B),
(Ⅰ)求由抛物线
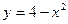 与直线
与直线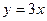 所围成的图形面积;
所围成的图形面积;(Ⅱ)求使⊿PAB的面积为最大时P点的坐标。
(Ⅰ)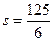 (Ⅱ)P点的坐标为
(Ⅱ)P点的坐标为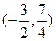 时,⊿PAB的面积最大
时,⊿PAB的面积最大
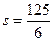 (Ⅱ)P点的坐标为
(Ⅱ)P点的坐标为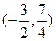 时,⊿PAB的面积最大
时,⊿PAB的面积最大 (Ⅰ)由 解得
解得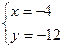 或
或
即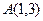 ,B
,B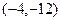 ----------------2分
----------------2分
因此所求图形的面积为
 ------------4分
------------4分
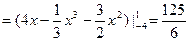 -------------6分
-------------6分
(Ⅱ)设点P的坐标为(a,b)由(Ⅰ)得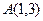 ,B
,B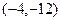
要使⊿PAB的面积最大即使点P到直线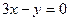 的距离最大 -------8分
的距离最大 -------8分
故过点P的切线与直线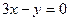 平行
平行
又过点P的切线得斜率为 -------10分
-------10分
 即
即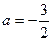 ,
,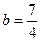
∴P点的坐标为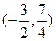 时,⊿PAB的面积最大。 --------13分
时,⊿PAB的面积最大。 --------13分
 解得
解得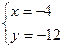 或
或
即
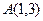 ,B
,B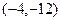 ----------------2分
----------------2分因此所求图形的面积为
 ------------4分
------------4分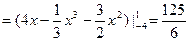 -------------6分
-------------6分(Ⅱ)设点P的坐标为(a,b)由(Ⅰ)得
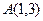 ,B
,B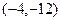
要使⊿PAB的面积最大即使点P到直线
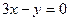 的距离最大 -------8分
的距离最大 -------8分故过点P的切线与直线
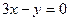 平行
平行又过点P的切线得斜率为
 -------10分
-------10分 即
即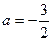 ,
,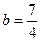
∴P点的坐标为
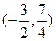 时,⊿PAB的面积最大。 --------13分
时,⊿PAB的面积最大。 --------13分
练习册系列答案
 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
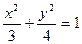 的焦点F与抛物线C:
的焦点F与抛物线C: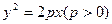 的焦点关于直线x-y=0
的焦点关于直线x-y=0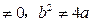 ),M是抛物线C上的点,设直线AM,
),M是抛物线C上的点,设直线AM,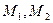 .求证:当M点在抛物线上变动时(只要
.求证:当M点在抛物线上变动时(只要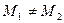 )直线
)直线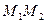 恒过一定点,并求出这个定点的坐标.
恒过一定点,并求出这个定点的坐标.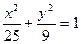 的右准线是抛物线的准线,抛物线的顶点是原点,求抛物线方程
的右准线是抛物线的准线,抛物线的顶点是原点,求抛物线方程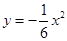 的准线方程为 。
的准线方程为 。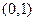 与抛物线
与抛物线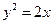 有且只有一个公共点的直线的条数是( )
有且只有一个公共点的直线的条数是( )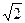
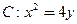 上一点P到定点A(0,1)的距离为2,则点P到
上一点P到定点A(0,1)的距离为2,则点P到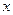
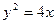 上一点
上一点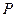 引其准线的垂线,垂足为
引其准线的垂线,垂足为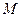 ,设抛物线的焦点为
,设抛物线的焦点为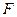 ,且
,且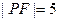 ,则
,则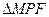 的面积为
的面积为
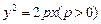 的焦点为
的焦点为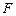 ,准线
,准线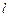 与
与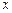 轴交于点
轴交于点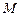 ,若
,若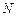 为
为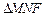 为等腰三角形,
为等腰三角形,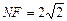 时,则
时,则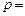 _____.
_____.