题目内容
【题目】已知中心在原点的椭圆C的一个顶点为![]() ,焦点在x轴上,右焦点到直线
,焦点在x轴上,右焦点到直线![]() 的距离为
的距离为![]() .
.
![]() 求椭圆的标准方程;
求椭圆的标准方程;
![]() 若直线l:
若直线l:![]() 交椭圆C于M,N两点,设点N关于x轴的对称点为
交椭圆C于M,N两点,设点N关于x轴的对称点为![]() 点
点![]() 与点M不重合
与点M不重合![]() ,且直线
,且直线![]() 与x轴的交于点P,求
与x轴的交于点P,求![]() 的面积的最大值.
的面积的最大值.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
![]() 由题意可知,椭圆是焦点在x轴上的椭圆,并求得b,再由点到直线的距离公式求得c,由隐含条件求得a,则椭圆方程可求;
由题意可知,椭圆是焦点在x轴上的椭圆,并求得b,再由点到直线的距离公式求得c,由隐含条件求得a,则椭圆方程可求;
![]() 联立直线方程与椭圆方程,化为关于y的一元二次方程,利用根与系数的关系求得M,N的纵坐标的和与积,再求出P的坐标,写出三角形面积公式,利用基本不等式求最值.
联立直线方程与椭圆方程,化为关于y的一元二次方程,利用根与系数的关系求得M,N的纵坐标的和与积,再求出P的坐标,写出三角形面积公式,利用基本不等式求最值.
解:![]() 依题意可设椭圆方程为
依题意可设椭圆方程为![]() ,
,![]() .
.
设右焦点![]() ,
,
由题设条件:![]() ,解得
,解得![]() ,
,
![]() .
.
故所求椭圆方程为:![]() ;
;
![]() 设
设![]() ,
,![]() ,
,
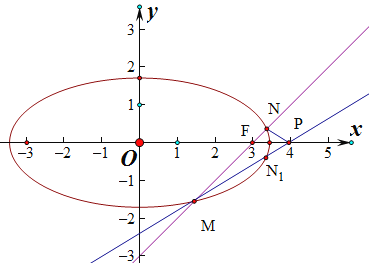
联立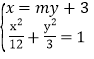 ,得
,得![]() .
.
![]() ,
,![]() ,
,
由题设知,![]() ,
,![]() 直线
直线![]() 的方程为
的方程为![]() .
.
令![]() ,得
,得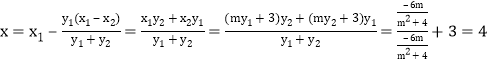 .
.
![]() 点P坐标为
点P坐标为![]() .
.
![]()
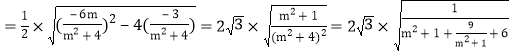
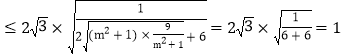 .
.
![]() 当且仅当
当且仅当![]() ,即
,即![]() 时等号成立
时等号成立![]() .
.
![]() 的面积的最大值为1.
的面积的最大值为1.

练习册系列答案
相关题目
【题目】2019年是新中国成立70周年,也是全面建成小康社会的关键之年.为喜迎祖国70周年生日,全民齐心奋力建设小康社会,某校特举办“喜迎国庆,共建小康”知识竞赛活动.下面的茎叶图是参赛两组选手的答题得分情况,则下列说法正确的是( )
甲 | 乙 | |||||
5 | 7 | 7 | ||||
7 | 3 | 2 | 8 | 3 | 4 | 5 |
3 | 9 | 1 | ||||
A.甲组选手得分的平均数小于乙组选手得分的平均数.
B.甲组选手得分的中位数大于乙组选手得分的平均数.
C.甲组选手得分的中位数等于乙组选手得分的中位数.
D.甲组选手得分的方差大于乙组选手得分的方差.