题目内容
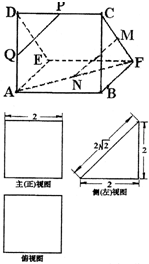
一个多面体的直观图及三视图如图所示:(其中M、N、P、Q分别是FC、AF、DC、AD的中点)
(1)直线DE与直线BF的位置关系是什么、夹角大小为多少?
(2)判断并证明直线MN与直线PQ的位置关系;
(3)求三棱锥D-ABF的体积.
(1)直线DE与直线BF的位置关系是什么、夹角大小为多少?
(2)判断并证明直线MN与直线PQ的位置关系;
(3)求三棱锥D-ABF的体积.

(1)由三视图分析得到原图形为两个侧面垂直的直三棱柱的平放图形,由图可知直线DE与直线BF的位置关系是异面直线,其夹角为∠BFC,大小为45°;
(2)直线MN与直线PQ的位置关系是平行
证明:连接AC,因为M、N、P、Q分别是FC、AF、DC、AD的中点,所以PQ∥AC,MN∥AC,所以MN∥PQ;
(3)由三视图可知△ABF是边长为2的等腰直角三角形,且三棱锥D-ABF的高为AD=2,
所以VD-ABF=
×S△ABF×AD=
×
×2×2×2=
.
(2)直线MN与直线PQ的位置关系是平行
证明:连接AC,因为M、N、P、Q分别是FC、AF、DC、AD的中点,所以PQ∥AC,MN∥AC,所以MN∥PQ;
(3)由三视图可知△ABF是边长为2的等腰直角三角形,且三棱锥D-ABF的高为AD=2,
所以VD-ABF=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 4 |
| 3 |

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
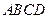 是直角梯形,角DABS是直角,
是直角梯形,角DABS是直角,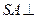 面
面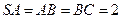 ,
,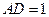 ,求面
,求面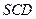 和面
和面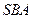 所成角的正切值.
所成角的正切值.
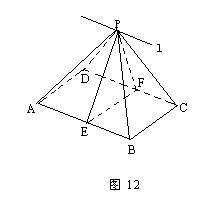
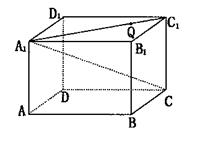
 .(1)求直线A1C与D1C1所成角的正切值;(2)在线段A1C上有一点Q,且C1Q=
.(1)求直线A1C与D1C1所成角的正切值;(2)在线段A1C上有一点Q,且C1Q= C1A1,求平面QDC与平面A1DC所成锐二面角的大小.
C1A1,求平面QDC与平面A1DC所成锐二面角的大小.