题目内容
【题目】△ABC的三个内角A,B,C的对边分别是a,b,c,则: ①若cosBcosC>sinBsinC,则△ABC一定是钝角三角形;
②若acosA=bcosB,则△ABC为等腰三角形;
③ ![]() ,
, ![]() ,若
,若 ![]() ,则△ABC为锐角三角形;
,则△ABC为锐角三角形;
④若O为△ABC的外心, ![]() ;
;
⑤若sin2A+sin2B=sin2C, ![]() ,
, 
以上叙述正确的序号是 .
【答案】①③④⑤
【解析】解:①若cosBcosC>sinBsinC,则cosBcosC﹣sinBsinC=cos(B+C)>0,
即﹣cosA>0,cosA<0,则∠A为钝角,故△ABC一定是钝角三角形,正确.②若acosA=bcosB,则由正弦定理得2rsinAcosA=2rsinBcosB,即sin2A=sin2B,则2A=2B或2A+2B=180,即A=B或A+B=90°,则△ABC为等腰三角形或直角三角形,错误;③ ![]() ,
, ![]() ,
,
则 ![]() =tanA+tanB+tanC=(1﹣tanAtanB)tan(A+B)+tanC>0
=tanA+tanB+tanC=(1﹣tanAtanB)tan(A+B)+tanC>0
tan(A+B)+tanC>tanAtanBtan(A+B)0>tanAtanBtan(A+B)
∴必有A+B> ![]() ,且A,B都为锐角
,且A,B都为锐角
∴C也必为锐角,
∴△ABC为锐角三角形,正确,④O为△ABC的外心, ![]()
![]() =
= ![]() (
( ![]() ﹣
﹣ ![]() )=
)= ![]()
![]() ﹣
﹣ ![]()
![]() ,
,
=| ![]() ||
|| ![]() |cos<
|cos< ![]() ,
, ![]() >﹣|
>﹣| ![]() ||
|| ![]() |cos<
|cos< ![]() ,
, ![]() >=
>= ![]() |
| ![]() |2﹣
|2﹣ ![]() |
| ![]() |2=
|2= ![]() (b2﹣c2),正确,⑤若sin2A+sin2B=sin2C,则由正弦定理得a2+b2=c2,则△ABC是直角三角形,
(b2﹣c2),正确,⑤若sin2A+sin2B=sin2C,则由正弦定理得a2+b2=c2,则△ABC是直角三角形,
∴( ![]() ﹣
﹣ ![]() )(
)( ![]() ﹣
﹣ ![]() )=0,
)=0,
∴ ![]() ﹣
﹣ ![]() (
( ![]() +
+ ![]() )+
)+ ![]() =0,∴
=0,∴ ![]() =﹣2
=﹣2 ![]() ,
,
∵﹣ ![]() =
= ![]() +
+ ![]() ,∴
,∴ ![]() 2=
2= ![]() 2+
2+ ![]() 2+2
2+2 ![]() ,∴5
,∴5 ![]() 2=
2= ![]() 2+
2+ ![]() 2,即结论成立.
2,即结论成立.
所以答案是①③④⑤.

【题目】某医疗科研项目对5只实验小白鼠体内的A、B两项指标数据进行收集和分析,得到的数据如下表:
指标 | 1号小白鼠 | 2号小白鼠 | 3号小白鼠 | 4号小白鼠 | 5号小白鼠 |
A | 5 | 7 | 6 | 9 | 8 |
B | 2 | 2 | 3 | 4 | 4 |
(1)若通过数据分析,得知A项指标数据与B项指标数据具有线性相关关系,试根据上表,求B项指标数据y关于A项指标数据x的线性回归方程 ![]() =
= ![]() x+
x+ ![]() ;
;
(2)现要从这5只小白鼠中随机抽取3只,求其中至少有一只B项指标数据高于3的概率. 参考公式: ![]() =
= 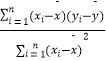 =
=  ,
, ![]() =
= ![]() ﹣
﹣ ![]() .
.