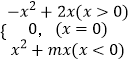��Ŀ����
����Ŀ����֪����{an}��{bn}�ֱ�����a1=1��|an+1��an|=2���� ![]() |=2������n��N* �� ������{an}��{bn}��ǰn��ͷֱ�ΪSn �� Tn ��
|=2������n��N* �� ������{an}��{bn}��ǰn��ͷֱ�ΪSn �� Tn ��
��1��������{an}��{bn}���ǵ������У�������{an}��{bn}��ͨ�ʽ��
��2��������{cn}���㣺����Ψһ��������k��k��2����ʹ��ck��ck��1 �� �������{cn}Ϊ��k�����С��� ��������{an}Ϊ��5�����С�����Sn��
��������{an}Ϊ��p�����С�������{bn}Ϊ��q�����С����Ƿ����������mʹ��Sm+1=Tm�������ڣ����m�����ֵ���������ڣ���˵�����ɣ�
���𰸡�
��1���⣺������{an}��{bn}��Ϊ�������У�
���ɵ���ʽ�ɵ�an+1��an=2��b2=��2b1=2��bn+2=2bn+1��n��N*��
������{an}Ϊ�Ȳ����У�����{bn}�ӵڶ����ɵȱ����У�
��an=2n��1��bn= ![]()
��2���⣺�١�����{an}���㣺����Ψһ��������k=5��ʹ��ak��ak��1����|an+1��an|=2��
������{an}��Ϊ1��3��5��7��5��7��9��11������
��ǰ4��Ϊ����Ϊ1������Ϊ2�ĵȲ����У��ӵ�5�ʼΪ����5������Ϊ2�ĵȲ����У�
��Sn=  ��
��
�ڡ�| ![]() |=2����bn+1=��2bn��
|=2����bn+1=��2bn��
��|bn|=2n��1��
������{bn}Ϊ��q�����С���b1=��1��
������{bn}������ֻ���������
�������������m��ʹ��Sm+1=Tm����Ȼm��1����TmΪ������
��{an}�и����Ϊ������
��m��Ϊż����
��Sm+1��1+3+��+��2m+1��=��m+1��2��
��q��mʱ��Tm=��1+2+4+��+2m��2+2m��1=2m��3��
��m��6ʱ��2m��3����m+1��2���ʲ�����������mʹ��Sm+1=Tm��
��q=mʱ��Tm=��1+21+��+2m��2+����2m��1��=��3��0��
��Ȼ������������mʹ��Sm+1=Tm��
��q��mʱ���ࣨTm��min=��1+21+��+2m��3+����2m��2��+2m��1=2m��1��3��
��2m��1��3����m+1��2���Ŵ���������mʹ��Sm+1=Tm��
��m��6��
��m=6ʱ��q��6��
���죺{an}Ϊ1��3��1��3��5��7��9������{bn}Ϊ��1��2��4��8����16��32��64����
��ʱp=3��q=5��
��mmax=6����Ӧ��p=3��q=5
����������1����������Ϊ�������У���ϵ���ʽ�ɵ�an+1��an=2��b2=��2b1��bn+2=2bn+1��n��N*���ɴ˿ɵ�����{an}Ϊ�Ȳ����У�����{bn}�ӵڶ����ɵȱ����У�Ȼ�����õȲ����к͵ȱ����е�ͨ�ʽ��ô𰸣���2���ٸ�����Ŀ�����жϣ�����{an}��Ϊ1��3��5��7��5��7��9��11��������ǰ4��Ϊ����Ϊ1������Ϊ2�ĵȲ����У��ӵ�5�ʼΪ����5������Ϊ2�ĵȲ����У����Sn���ɣ�����������{bn}Ϊ�������С���b1=��1���ۺ��ж�����{bn}������ֻ����������������������m��ʹ��Sm+1=Tm����Ȼm��1����TmΪ��������{an}�и����Ϊ�������ɵ�m��Ϊż����������q��m��q=m��q��m��֤��m��6��������м��ɣ�
�����㾫�����������е�ǰn��ͺ����е�ͨ�ʽ�ǽ����ĸ�������Ҫ֪������{an}��ǰn���sn��ͨ��an�Ĺ�ϵ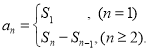 ���������an�ĵ�n����n֮��Ĺ�ϵ������һ����ʽ��ʾ����ô�����ʽ�ͽ�������е�ͨ�ʽ��
���������an�ĵ�n����n֮��Ĺ�ϵ������һ����ʽ��ʾ����ô�����ʽ�ͽ�������е�ͨ�ʽ��

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�