题目内容
7.已知函数f(x)=-x+$\frac{m}{x}$-1(x≠0).(1)当m=2时,判断f(x)在(-∞,0)的单调性,并用定义证明.
(2)若对任意x∈(-∞,0),不等式f(x)>0恒成立,求m的取值范围.
分析 (1)当m=2时,函数f(x)=-x+$\frac{2}{x}$-1在(-∞,0)递减.运用单调性的定义证明,注意作差、变形和定符号、下结论几个步骤;
(2)由题意可得m<x2+x在x<0恒成立,运用二次函数的最值的求法,可得最小值,进而得到m的范围.
解答 解:(1)当m=2时,函数f(x)=-x+$\frac{2}{x}$-1在(-∞,0)递减.
证明:设x1<x2<0,则f(x1)-f(x2)=(-x1-1+$\frac{2}{{x}_{1}}$)-(-x2-1+$\frac{2}{{x}_{2}}$)
=(x2-x1)(1+$\frac{2}{{x}_{1}{x}_{2}}$),由x1<x2<0,可得x2-x1>0,
1+$\frac{2}{{x}_{1}{x}_{2}}$>0,即有f(x1)-f(x2)>0,
故f(x)在(-∞,0)为减函数;
(2)任意x∈(-∞,0),不等式f(x)>0恒成立,
即为m<x2+x在x<0恒成立,
由y=x2+x=(x+$\frac{1}{2}$)2-$\frac{1}{4}$,
当x=-$\frac{1}{2}$时,取得最小值-$\frac{1}{4}$,
即为m<-$\frac{1}{4}$.则m的取值范围是(-∞,-$\frac{1}{4}$).
点评 本题考查函数的单调性的判断和证明,考查不等式恒成立问题的解法,注意运用参数分离和二次函数的最值的求法,属于中档题.

练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
18.如图,半径为R的球O中有一内接圆柱,当圆柱的侧面积最大时,球的体积与该圆柱的体积之比是( )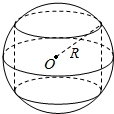

| A. | $\frac{4}{3}$ | B. | $\frac{4\sqrt{2}}{3}$ | C. | $\sqrt{2}$ | D. | $\frac{\sqrt{2}}{3}$ |
 如图,在空间四边形ABCD中,连接AC,BD,E,F分别是边AC.BD的中点,设$\overrightarrow{AB}$=$\overrightarrow{a}$-2$\overrightarrow{c}$,$\overrightarrow{CD}$=5$\overrightarrow{a}$+6$\overrightarrow{b}$-8$\overrightarrow{c}$,试用$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$表示$\overrightarrow{EF}$.
如图,在空间四边形ABCD中,连接AC,BD,E,F分别是边AC.BD的中点,设$\overrightarrow{AB}$=$\overrightarrow{a}$-2$\overrightarrow{c}$,$\overrightarrow{CD}$=5$\overrightarrow{a}$+6$\overrightarrow{b}$-8$\overrightarrow{c}$,试用$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$表示$\overrightarrow{EF}$.