题目内容
17．已知实数x，y满足y=x2-x+2（-1≤x≤1），试求$\frac{y+3}{x+2}$的最大值和最小值．分析 通过$\frac{y+3}{x+2}$=$\frac{y-（-3）}{x-（-2）}$的几何意义，画出抛物线y=x2-x+2（-1≤x≤1），通过观察求得斜率，最值即可得到．
解答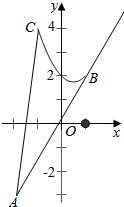 
解：$\frac{y+3}{x+2}$=$\frac{y-（-3）}{x-（-2）}$表示抛物线y=x2-x+2（-1≤x≤1）上的点（x，y）
与点A（-2，-3）的斜率，
作出抛物线y=x2-x+2（-1≤x≤1），C（-1，4），B（1，2），
连接AC，AB，可得kAC=$\frac{4-（-3）}{-1-（-2）}$=7，
kAB=$\frac{2-（-3）}{1-（-2）}$=$\frac{5}{3}$，
由图象可得$\frac{y+3}{x+2}$的最大值为7，
最小值为$\frac{5}{3}$．
点评 本题考查直线的斜率的应用，属于简单的线性规划的应用，考查计算能力，属于基础题．
练习册系列答案
相关题目