题目内容
12.复平面上复数z对应的点Z在曲线|z-1|=2上,求复数2z-1-i在复平面上对应点的轨迹方程.(化成直角坐标方程)分析 设出复数2z-1-i在复平面上对应点,然后利用已知条件化简求解即可.
解答 解:设复数2z-1-i在复平面上对应点为:(x,y).
即2z-1-i=x+yi,
可得2(z-1)=(x-1)+(y+1)i,|z-1|=2,
可得|(x-1)+(y+1)i|=4.
即:$\sqrt{{(x-1)}^{2}+{(y+1)}^{2}}$=4.
可得:(x-1)2+(y+1)2=16.
复数2z-1-i在复平面上对应点的轨迹方程:(x-1)2+(y+1)2=16.
点评 本题考查复数对应点的轨迹方程的求法,考查计算能力.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
20.A为三角形ABC的一个内角.若sinA+cosA=$\frac{12}{25}$,2sinBcosC=sinA,则这个三角形的形状不可能为( )
| A. | 锐角三角形 | B. | 钝角三角形 | ||
| C. | 等腰且钝角三角形 | D. | 等腰三角形 |
7.已知函数f(x)=$\left\{\begin{array}{l}{{x}^{2}+x+a}&{x<0}\\{lnx}&{x>0}\end{array}\right.$,若函数f(x)的图象在点A、B处的切线重合,则a的取值范围是( )
| A. | (-1,+∞) | B. | (-ln2,+∞) | C. | (-2,-1) | D. | (1,2) |
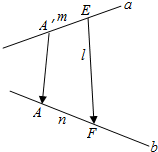 如图,两条异面直线a,b所成的角为θ,在直线a,b上分别取点A′,E和点A,F,使AA′⊥a,且AA′⊥b(AA′称为异面直线a,b的公垂线),已知A′E=m,AF=n,EF=l,求公垂线AA′的长.
如图,两条异面直线a,b所成的角为θ,在直线a,b上分别取点A′,E和点A,F,使AA′⊥a,且AA′⊥b(AA′称为异面直线a,b的公垂线),已知A′E=m,AF=n,EF=l,求公垂线AA′的长.